Предмет: Алгебра,
автор: rrrrtttt01
Решите уравнение...............................................
Приложения:
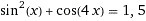
Ответы
Автор ответа:
4
Понизим степень и применим формулу косинуса двойного угла, имеем
Решим последнее уравнение как квадратное уравнение относительно cos2x
- уравнение решений не имеет
Похожие вопросы
Предмет: Алгебра,
автор: playpilinok
Предмет: Литература,
автор: olesyailchenko
Предмет: Информатика,
автор: asslsclc
Предмет: Химия,
автор: AlbegovaSabinka
Предмет: История,
автор: angelinakuzya