Предмет: Геометрия,
автор: andrijnagorny
ПОМОГИТЕ!!! ДАЮ 30 БАЛЛОВ!!!
О - точка пересечения биссектрис треугольника АВС. Радиусы кругов, описанных вокруг треугольников АВС и АОВ, равны 5 корней из 2 см и 5 см соответственно. Найдите величину угла С.
antonovm:
".Распишите здесь, какими действиями Вы дошли до такого ответа." звучит как приказ
Нет, не приказываю :)
ну тогда можно было добавить пожалуйста , уважаемый Миша
Аndrijnagorny, скажите, пожалуйста, Ваше задание записано правильно? )
Задание записано правильно
По теор. синусов: AB/sinC=10√2; AB/sin(AOB)=10 =>
√2sinC=sin(AOB)
AOB=90+C/2 (угол между биссектрисами): 4sin^2(C)=1+cosC <=>
4cos^2(C)+cosC-3 =0 <=> cosC=3/4 (cosC≠-1 т.к. C<180)
√2sinC=sin(AOB)
AOB=90+C/2 (угол между биссектрисами): 4sin^2(C)=1+cosC <=>
4cos^2(C)+cosC-3 =0 <=> cosC=3/4 (cosC≠-1 т.к. C<180)
да все так , но с трезубцем красивее
Согласен.
Если D - середина дуги AB описанной окружности ABC (с центром E), то по трилистнику D равноудалена от A, B, O. Тогда DB=5, EB=ED=5√2, из △BED cos(BED)=3/4. ∠C=∪AB/2=∠BED.
Если D - середина дуги AB описанной окружности ABC (с центром E), то по трилистнику D равноудалена от A, B, O. Тогда DB=5, EB=ED=5√2, из △BED cos(BED)=3/4. ∠C=∪AB/2=∠BED.
https://i.imgur.com/GlBhRrB.png
Вначале заметил этот способ, передумал, объяснять дольше...
Ответы
Автор ответа:
1
баллы мне не нужны , это так-развлечение
Приложения:
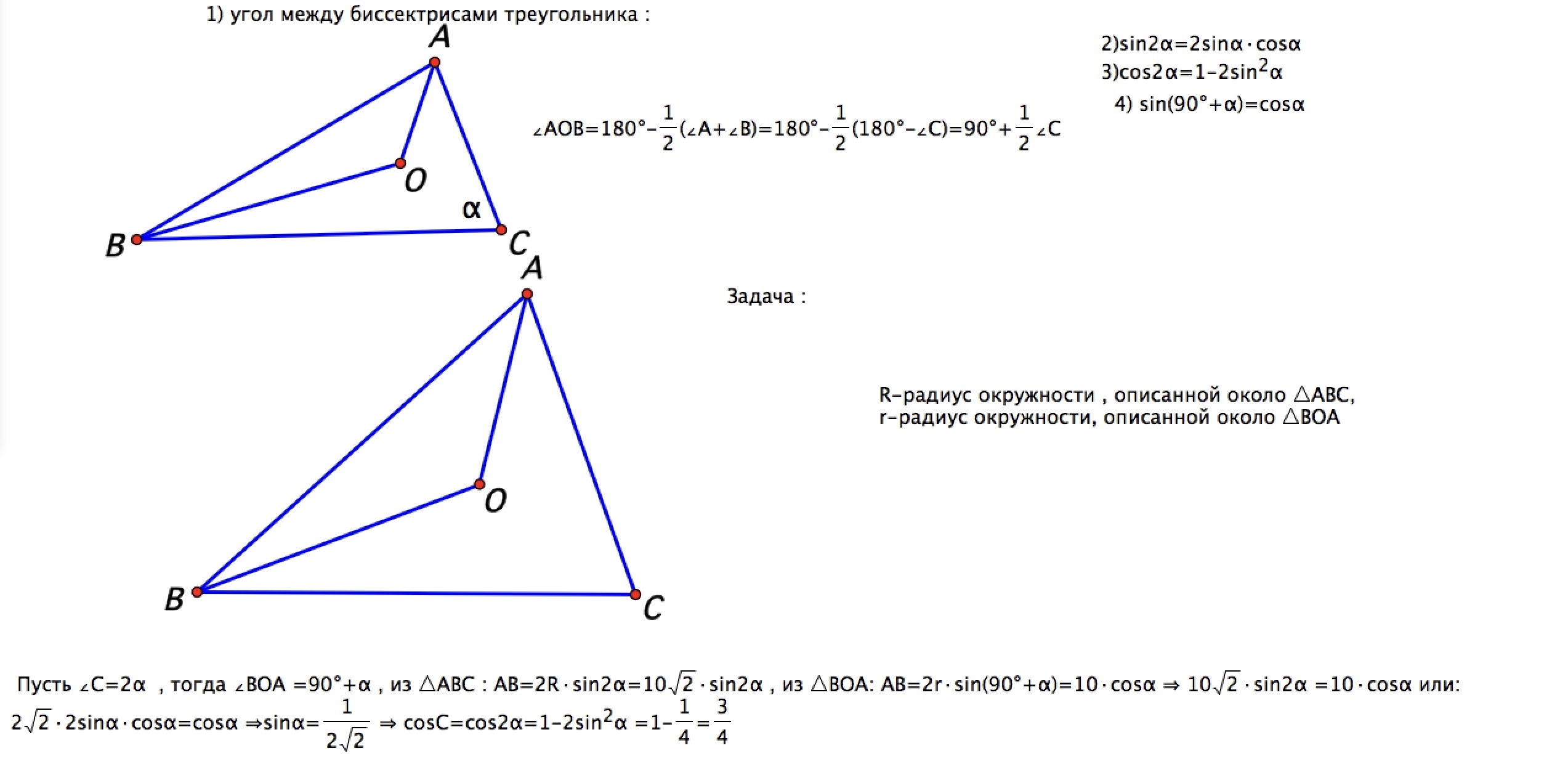
угол ВОА=90+альфа сейчас исправлю)
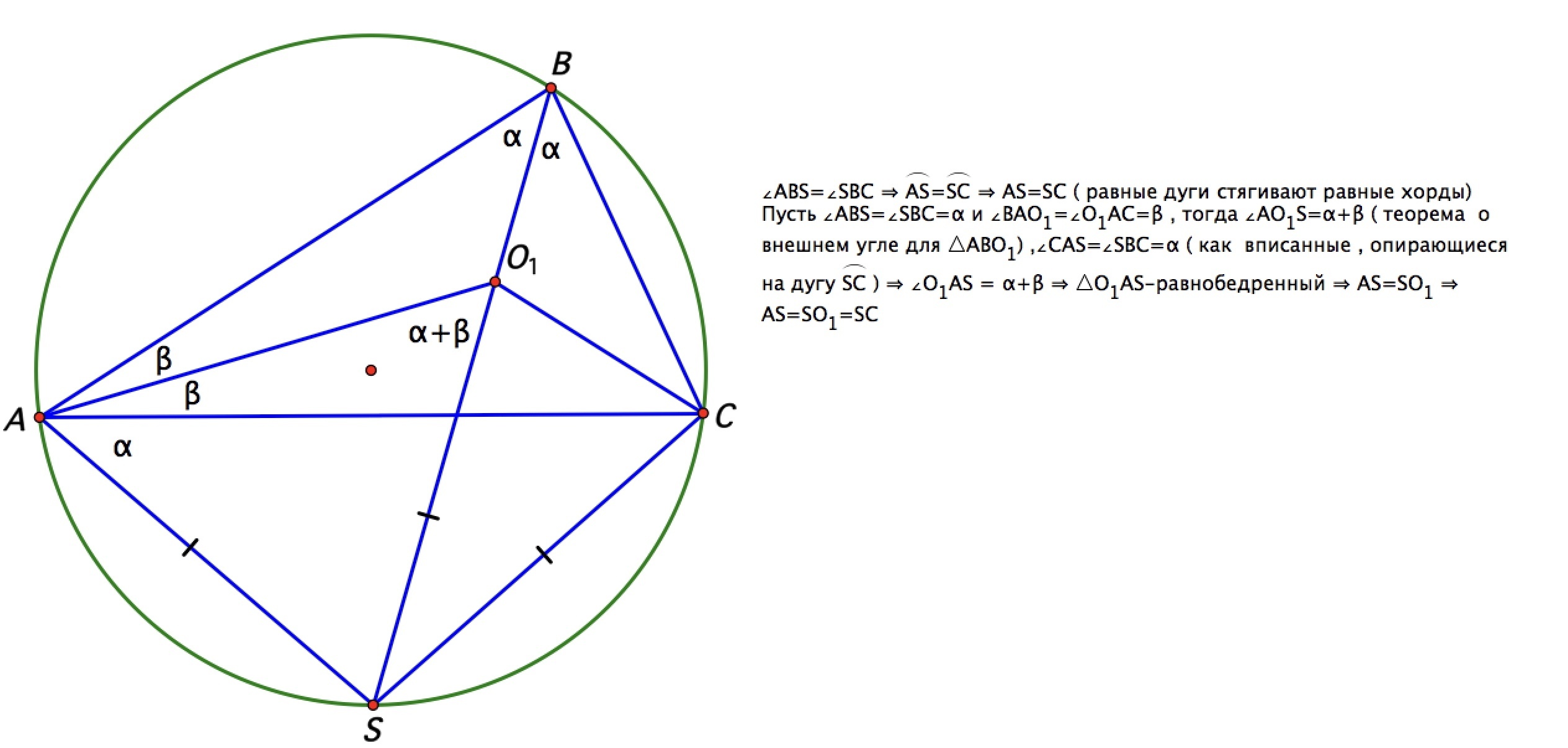
как дополнение -доказательство теоремы о трезубце , которую использовал Михаил
S-центр окружности , описанной около тр AO1C, а еще на этой окружности лежит центр вневписанной окружности , касающейся стороны АС ( небольшое обобщение)
Автор ответа:
2
А мы пойдём другим способом:
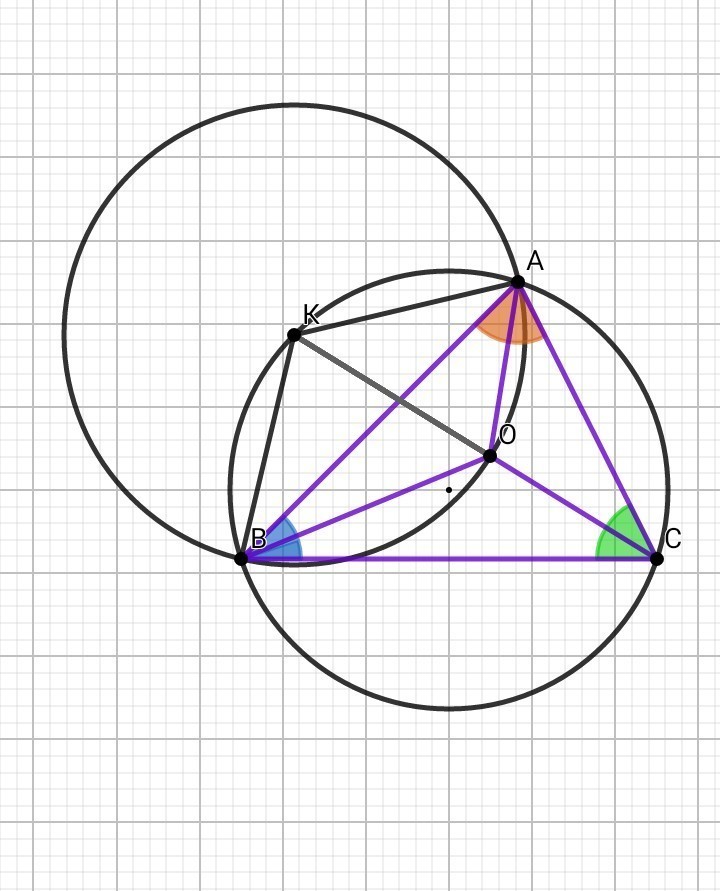
А) Рассмотрим рисунок 2 :
Пусть угол ВСО = а
Обозначим точку K, как точку пересечения прямой СО с окружностью, описанной около ∆ АВС, точка О – центр вписанной окружности ∆ АВС, тогда →
KB = KO = KA = 5 см - радиусы описанной окружности около треугольника АВО – по теореме о трилистнике или лемме о трезубце, или лемме Мансиона.
Рассмотрим ∆ ВКС:
По теореме синусов:
2R = BK / sin ВСО
2·5√2 = 5/ sina
sina = √2/4
cosC = cos2a = 1 – 2sin²a = 1 – 2·( √2/4 )² = 3/4 →
угол С = arccos( 3/4 )
Или можно поступить следующим образом:
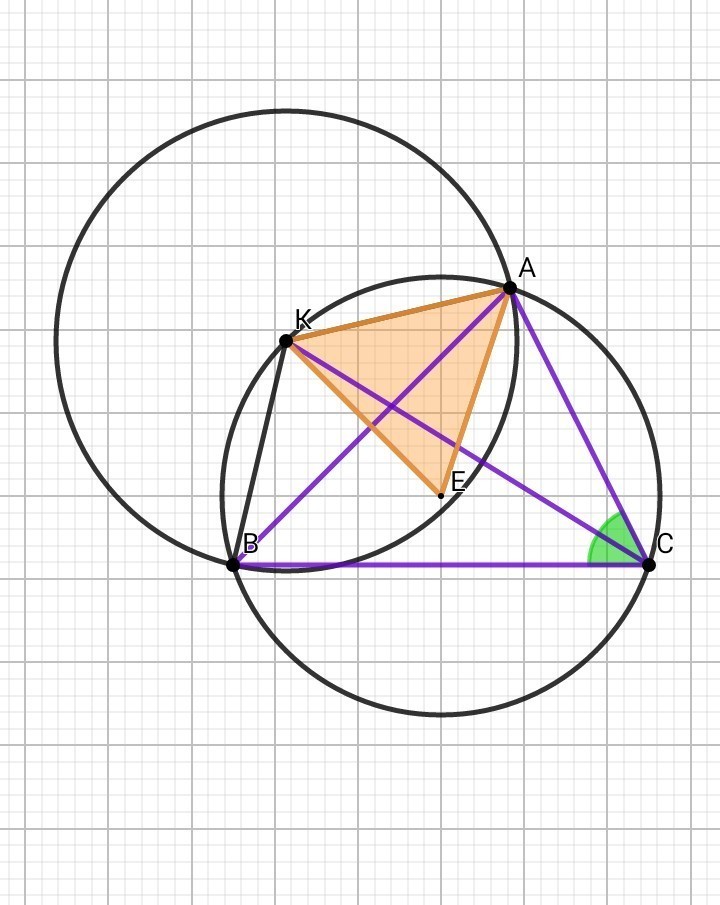
Б) Рассмотрим рисунок 1 :
точка Е - центр окружности, описанной около треугольника АВС
KE = AE = 5•( корень из 2 )
Рассмотрим тр. АКЕ:
По теореме косинусов:
АК^2 = АЕ^2 + КЕ^2 - 2• АЕ•КЕ•cos AEK
25 = 50 + 50 - 2•50•cos AEK
cos AEK = 3/4
угол АЕК = arccos( 3/4 )
Угол АСВ является вписанным углом окружности с центром в точке Е
▪Вписанный угол равен половине дуги, на которую этот угол опирается ▪
Угол АСВ = ( 1/2 ) • U AKB
U BK = U KA - равные хорды ВА и КА стягивают равные дуги
Угол АСВ = ( 1/2 ) • U AKB = U KA = U BK
Угол АКЕ является центральным углом окружности с центром в точке Е
▪ Центральный угол равен дуге, на которую этот угол опирается ▪
Угол АКЕ = U KA
Значит, угол АСВ = угол АКЕ = arccos( 3/4 )
Также если сделать замену:
r - радиус описанной окружности около треугольника АОВ
R - радиус описанной окружности около треугольника АВС , тогда
угол АСВ = arccos( ( 2R^2 - r^2 )/ 2R^2 )
ОТВЕТ: угол С = arccos( 3/4 )
А) Рассмотрим рисунок 2 :
Пусть угол ВСО = а
Обозначим точку K, как точку пересечения прямой СО с окружностью, описанной около ∆ АВС, точка О – центр вписанной окружности ∆ АВС, тогда →
KB = KO = KA = 5 см - радиусы описанной окружности около треугольника АВО – по теореме о трилистнике или лемме о трезубце, или лемме Мансиона.
Рассмотрим ∆ ВКС:
По теореме синусов:
2R = BK / sin ВСО
2·5√2 = 5/ sina
sina = √2/4
cosC = cos2a = 1 – 2sin²a = 1 – 2·( √2/4 )² = 3/4 →
угол С = arccos( 3/4 )
Или можно поступить следующим образом:
Б) Рассмотрим рисунок 1 :
точка Е - центр окружности, описанной около треугольника АВС
KE = AE = 5•( корень из 2 )
Рассмотрим тр. АКЕ:
По теореме косинусов:
АК^2 = АЕ^2 + КЕ^2 - 2• АЕ•КЕ•cos AEK
25 = 50 + 50 - 2•50•cos AEK
cos AEK = 3/4
угол АЕК = arccos( 3/4 )
Угол АСВ является вписанным углом окружности с центром в точке Е
▪Вписанный угол равен половине дуги, на которую этот угол опирается ▪
Угол АСВ = ( 1/2 ) • U AKB
U BK = U KA - равные хорды ВА и КА стягивают равные дуги
Угол АСВ = ( 1/2 ) • U AKB = U KA = U BK
Угол АКЕ является центральным углом окружности с центром в точке Е
▪ Центральный угол равен дуге, на которую этот угол опирается ▪
Угол АКЕ = U KA
Значит, угол АСВ = угол АКЕ = arccos( 3/4 )
Также если сделать замену:
r - радиус описанной окружности около треугольника АОВ
R - радиус описанной окружности около треугольника АВС , тогда
угол АСВ = arccos( ( 2R^2 - r^2 )/ 2R^2 )
ОТВЕТ: угол С = arccos( 3/4 )
Приложения:
" Почему КВ, КА, КО радиусы описанной окружности около ∆ АВО? " Теорема о трилистнике даёт точное обоснование ответу.
НЕТ , ТЕОРЕМА доказывает равенство этих отрезков, но почему они должны быть равны 5 , K-центр окружности , описанной около АВО ? а почему ?
Из этого равенства и вытекает, что КВ = КА = КО – радиусы. Точка К равноудалена от вершин ∆ АВО.
все , убедили , еще раз извините , замечательная теорема и доказывается не сложно , но школьники ее не знают
Как утверждил автор вопроса, он перешёл в математический класс. И теорему желательно знать)
согласен , желательно знать все теоремы(задачи) из книги Гордина "Теоремы и задачи школьной геометрии " , но боюсь наш школьник не поймет наших решений
буду рад ошибиться
очень красивое решение , но картинки не хватает
Скоро добавлю рисунок )
Добавил.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: natibunyakk
Предмет: Геометрия,
автор: dublyninm
Предмет: Математика,
автор: adelasi
Предмет: Геометрия,
автор: тёма113636