Круг разделен диаметром в два полукружия. В один из них вписаны два новых полукружия, которые опираются на радиус данного круга как на свой диаметр. В криволинейную фигуру, которая ограничена контурами этих трех полукружий, вписан круг. Во сколько раз его площадь меньше площади данного круга?
Ответы
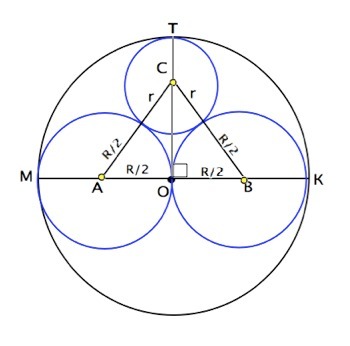
Пусть диаметр большого круга МК, О – его центр, радиус=R, А и В - центры полукружий, их радиусы АО=ОВ=R/2. Центр вписанного третьего круга С, его радиус – r.
Соединим центры полукружий с центром вписанного в криволинейную фигуру круга. Как вписанный, он касается внутренним касанием окружности большего круга и внешним - полукружий. АС=ВС=(R/2 + r). Треугольник АВС - равнобедренный. AO=BO, ⇒ СО - его медиана и высота. По т.Пифагора АС²=АО²+СО² Для удобства записи примем R/2=a. Тогда АО=а, R=ОТ=2а, СО=(2а-r). Запишем (a+r)²=a²+(2a-r)². ⇒ a²+2ar+r²=a²+4a²-4ar+r². ⇒ 4а²-6ar=0. Сократив уравнение на 2а, получим 2а-3r=0, ⇒ 3r=2a=R. Радиус вписанного круга равен R/3. Все круги - подобны. Для данных k=1/3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(R/3):S(R)=k²=(1/3)²=1/9. Ответ - в 9 раз площадь меньшего круга меньше площади большего круга.