Предмет: Алгебра,
автор: ipdwqujywpqiouweq
Решите уравнение............:
Приложения:
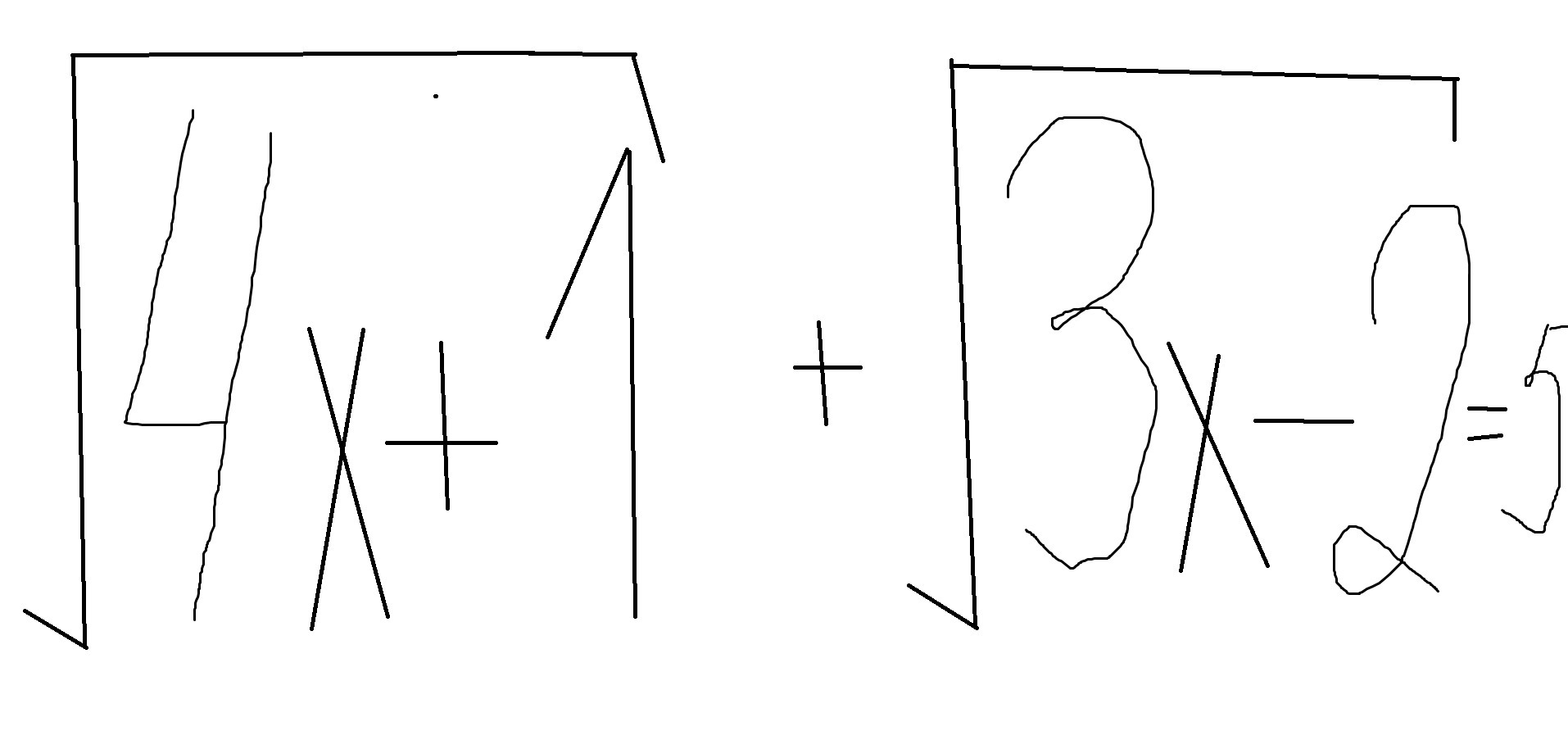
Ответы
Автор ответа:
3
ОДЗ:
Значит, ОДЗ для всего уравнения будет .
Проверим ОДЗ, возникшее по ходу решения:
Значит, новое ОДЗ для всего уравнения будет .
2 входит в ОДЗ, а 342 - не входит, поэтому правильный ответ 2.
Ответ:
Только 26-7x≥0 ⇒ x≤26/7, не больше
Поэтому 342 не подходит
И, кстати, да, это называется не "доп. ОДЗ", а "ОДЗ, возникшее по ходу решения". Это просто для ознакомления
Вопрос : А откуда 384? выходит же 364
Стоп, я что-то упустил?
А, все, нашел
Автор ответа:
2
Угадываем решение x=2 (при подстановке получаем 3+2=5). Поскольку левая часть уравнения монотонно возрастает, а правая постоянна, других решений быть не может.
Ответ: 2
Краткость - сестра таланта
"садитесь Петров - два !" сказал учитель семикласнику
я понимаю такие решения надо давать старшеклассникам, а средней школе надо ли ????
я понимаю такие решения надо давать старшеклассникам, а средней школе надо ли ????
Похожие вопросы
Предмет: Физкультура и спорт,
автор: ajymkadirsizova664
Предмет: Биология,
автор: rianaametova7
Предмет: Қазақ тiлi,
автор: kkltasheryt
Предмет: Математика,
автор: яяяяяяяя14
Предмет: Биология,
автор: AskSoudKek
одз можно дополнять
или можно без одз вообще, но в таком случае обязательно проверять корни
решайте как удобно и как знаете
удачи