Предмет: Математика,
автор: bestmusic
Помогите пожалуйста решить неравенство (решение обязательно)
Приложения:
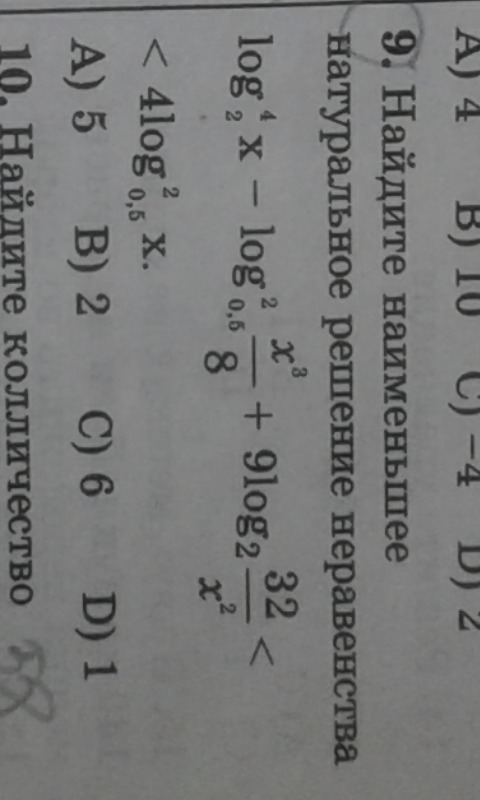
Ответы
Автор ответа:
1
ОДЗ: x > 0
_+_(1/8)_-_(1/4)_+__(4)_-_(8)_+_
Наим. натуральное решение 5
Ответ: 5
Похожие вопросы
Предмет: Английский язык,
автор: lord67063
Предмет: Другие предметы,
автор: aalua7
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Yenix