Предмет: Математика,
автор: gost1979
Вычислить двойной интеграл (с решением)
Приложения:

Аноним:
Ответ: 1/3
с решением
Ответы
Автор ответа:
10
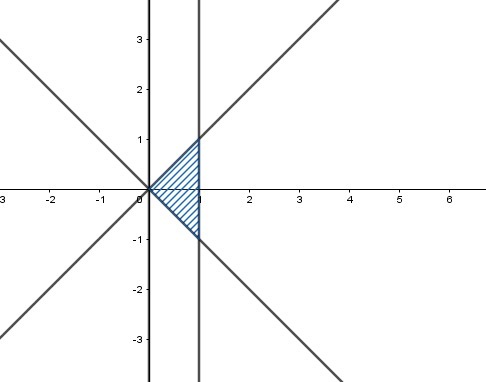
Интегрируем нашу функцию f(x,y) на множестве, заданном неравенствами 0 ≤ x ≤ 1 и −x ≤ y ≤ x .
P.S. интегралы которые решаются по частям решите Вы.. Для меня здесь долго)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kayne9772
Предмет: Русский язык,
автор: begalyevaazima
Предмет: Английский язык,
автор: kiraalimova00
Предмет: Алгебра,
автор: Аксентий
Предмет: Математика,
автор: настя5178