Предмет: Алгебра,
автор: ryanwolf2000
Решите уравнение и распишите подробно пожалуйста, очень нужно
Приложения:
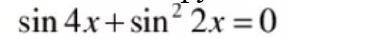
Ответы
Автор ответа:
1
sin 4x + sin²2x = 0
2sin2x · cos2x + sin²2x = 0
Разделим на cos²2x ≠ 0
2tg 2x + tg²2x = 0
tg2x·(2 + tg 2x) = 0
1) tg2x = 0 → 2x = πk → x1 = πk/2 k∈Z
2) 2 + tg 2x = 0 → tg 2x = -2 → 2x = -arctg 2 + πk →
→ x2 = -0.5arctg2 + 0.5πk k∈Z
Автор ответа:
1
sin(4x) + sin^2(2x) = 0
2sin(2x)cos(2x) + sin^2(2x) = 0
sin(2x)(2cos(2x) + sin(2x)) = 0
1) sin(2x) = 0
2x = πn
x = πn/2
2) 2cos(2x) + sin(2x) = 0
ctg(2x) = -1/2
2x = arcctg(-1/2) + πn
x = arcctg(-1/2)/2 + πn/2
Похожие вопросы
Предмет: Русский язык,
автор: bolat270411
Предмет: Математика,
автор: tkacenkoannamaria211
Предмет: Химия,
автор: galkinkirill15112007
Предмет: Геометрия,
автор: Дарина144
Предмет: Математика,
автор: natalyapost