помогите решить, найти произведение корней уравнения
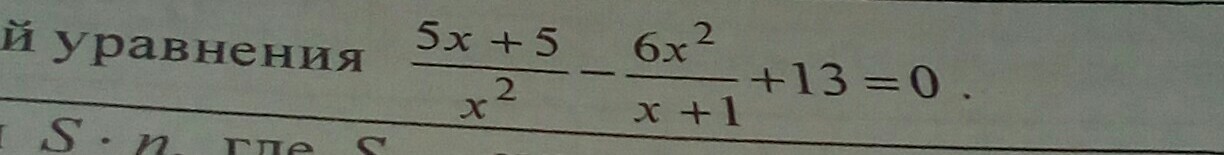
Ответы
Замена: (x+1)/x^2 = t. ОДЗ: х ≠ 0 и х ≠ -1.
При этих условиях получаем квадратное уравнение.
5t² + 13t - 6 = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:
D=13^2-4*5*(-6)=169-4*5*(-6)=169-20*(-6)=169-(-20*6)=169-(-120)=169+120=289;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√289-13)/(2*5)=(17-13)/(2*5)=4/(2*5)=4/10=0.4;
t_2=(-√289-13)/(2*5)=(-17-13)/(2*5)=-30/(2*5)=-30/10=-3.
Обратная замена.
1) t = 0,4 = 2/5 = (x + 10/x².
2x² - 5x - 5 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-5)^2-4*2*(-5)=25-4*2*(-5)=25-8*(-5)=25-(-8*5)=25-(-40)=25+40=65;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√65-(-5))/(2*2)=(√65+5)/(2*2)=(√65+5)/4;
x_2=(-√65-(-5))/(2*2)=(-√65+5)/(2*2)=(-√65+5)/4.
2) t = -3 = (x + 1)/x².
3x² + x + 1 = 0.
Ищем дискриминант:
D=1^2-4*3*1=1-4*3=1-12=-11;
Дискриминант меньше 0, уравнение не имеет корней.
Остаются 2 первых корня.
Их произведение равно ((√65+5)/4)*((-√65+5)/4) = (25 - 65)/16 = -40/16 =-2,5.