Предмет: Алгебра,
автор: pastuhsi
Доведіть, що √(4-2√3) = √3 - 1
Ответы
Автор ответа:
0
...........................
Приложения:
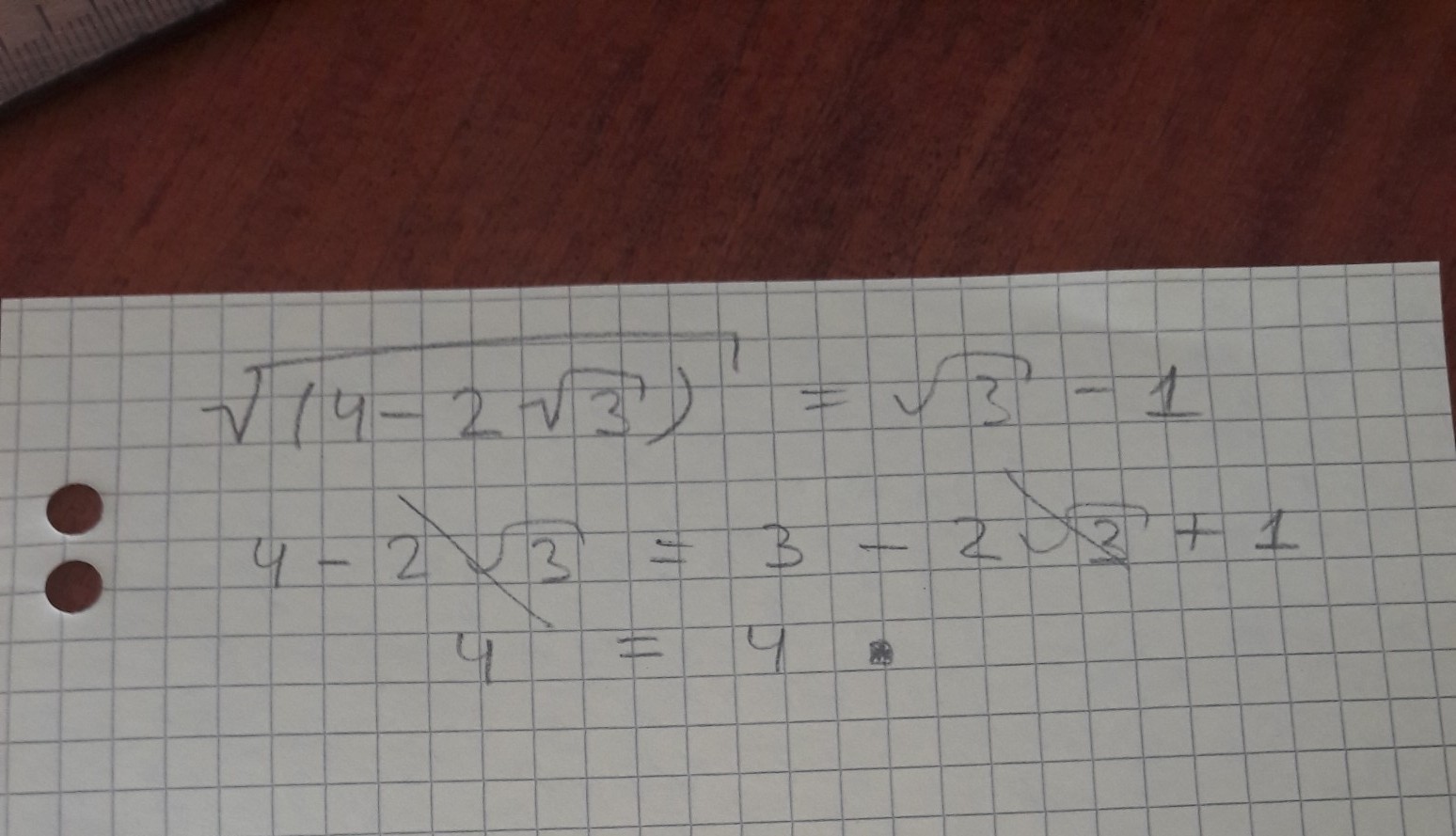
sergeymandcs:
В квадрат обе части возвёл
А тут доказательство как доказательство, просто пошли другим путем
Автор ответа:
0
Подивимося на те, що під корнем:

квадрат выражения под корнем равен самому числу, не точно использовалась формула сокращенного умножения
√(x²)=|x| - свойство корней четной степени
НО! (√x)²=x, x≥0
Это автору вопроса адресовано, рекомендую запомнить
Похожие вопросы
Предмет: Другие предметы,
автор: dianka20092
Предмет: Алгебра,
автор: noxxon
Предмет: Математика,
автор: noname1536
Предмет: История,
автор: пвпвпвпв
Предмет: Алгебра,
автор: nastyaery1