Помогите пожалуйста решить

Ответы
Данная задача может иметь 2 решения в зависимости от положения точки Д.
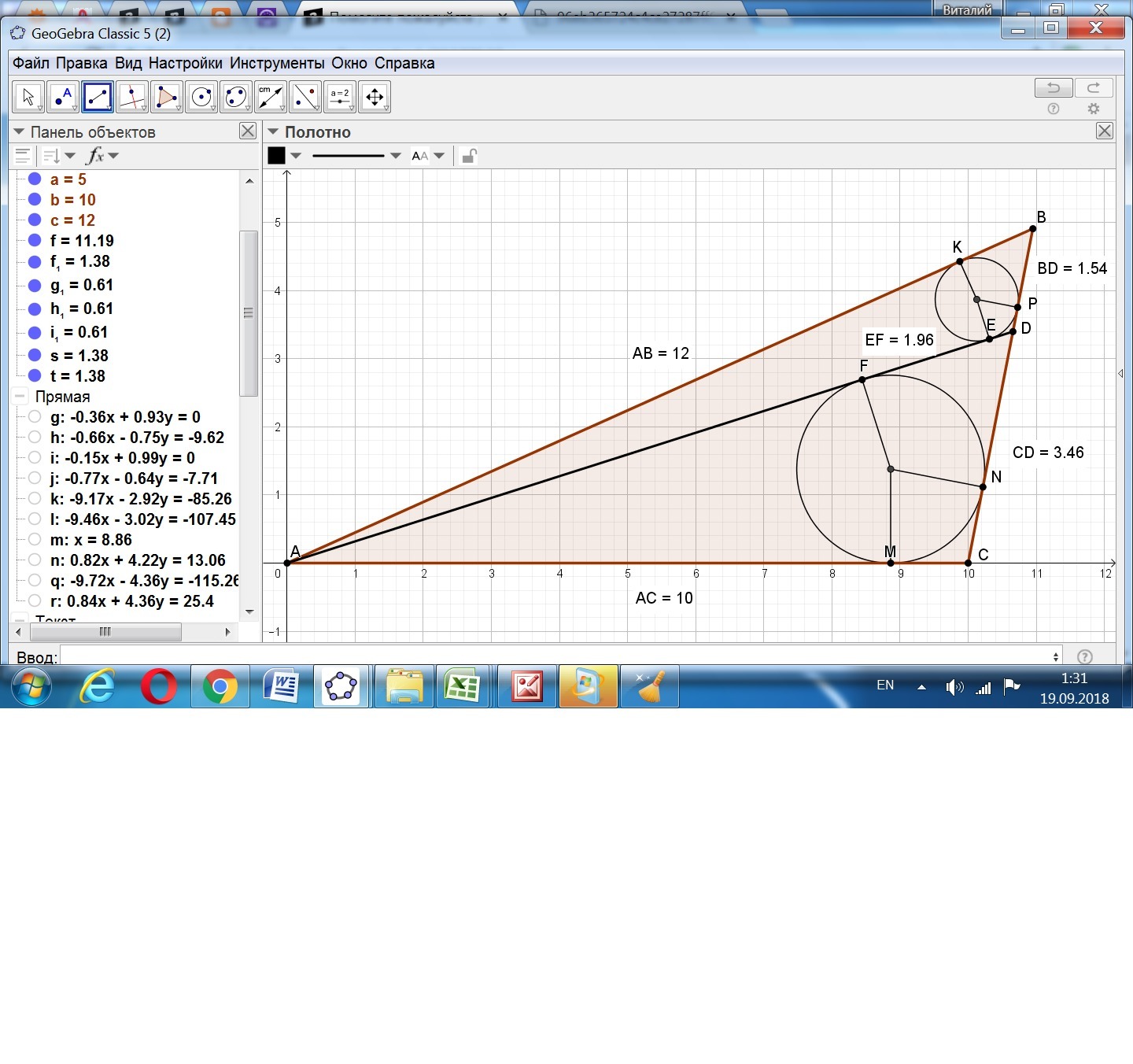
1) По 1 варианту точка Д находится на стороне ВС, которая разделена точкой Д на отрезки длиной (20/13) и (45/13).
Косинус угла В = (144 + 25 - 100)/(2*10*12) = 23/40.
Находим длину АД:
АД = √(144+(400/169)-2*12*(20/13)*(23/40)) = √125,1361 ≈ 11,18642.
Находим полупериметры и площади (по формуле Герона) треугольников АВД и АДС.
р(АВД) = 12,36244317, S = 7,552186246.
р(АДС) = 12,32398164, S = 16,99241669.
Отсюда находим радиусы вписанных окружностей: r = S/p.
r(АВД) = 0.610898, r(АДС) = 1.378829.
Находим углы ВАД и ДАС:
∠ВАД = 6,46060914°, ∠ДАС = 17,68623886°.
Далее по формуле L = r/(tg(α/2)) находим длины касательных от точки А до точек касания окружностей r1 и r2.
L1 = 10.82398, L2 = 8.862443.
Разность их и равна искомой длине: ΔL= 1,961539.
В этом варианте есть другой способ определения длины отрезка EF.
Используется свойство равенства длин касательных к окружности из одной точки.
EF = ДF - ДЕ = ДN - ДР = (ДС - СN) - (ВД - ВР).
Получили ЕF = (ДС - СМ) - (ВД - ВК).
С другой стороны ЕF = АЕ - АF = АК - АМ.
Просуммируем эти 2 уравнения:
2ЕF = (ДС - СМ) - (ВД - ВК) + АК - АМ.
Скомпонуем отрезки:
2ЕF = ДС - (СМ + АМ) + АВ - ВД.
Подставим значения: 2ЕF = (45/13) - 10 + 12 - (20/13) = 51/13.
Разделим на 2 и получаем ответ: ЕF = 51/26 ≈ 1,961538, который совпадает с предыдущим.
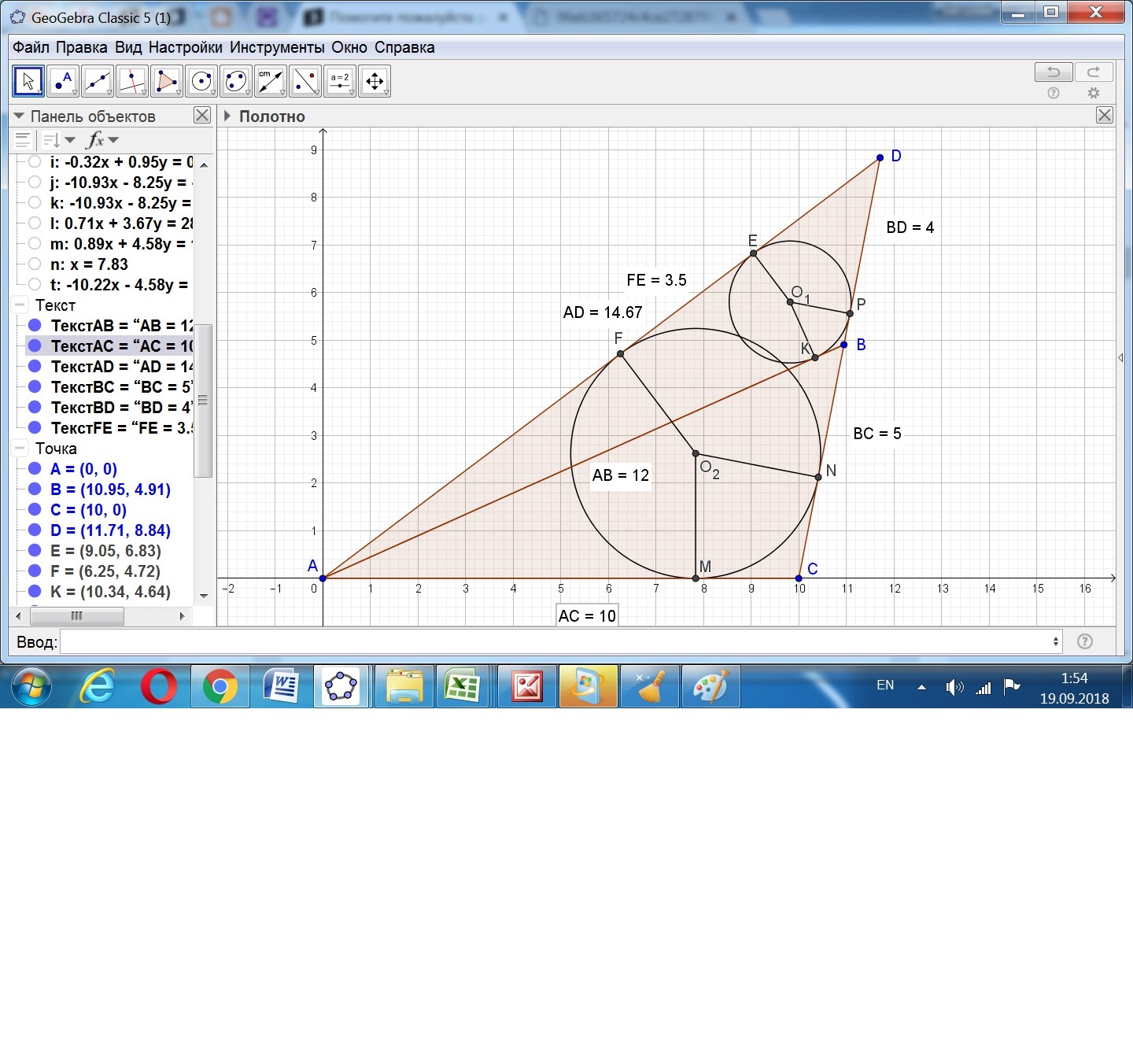
2) Аналогично рассмотрим второй вариант, когда точка Д находится на продолжении стороны ВС.
ЕF = РN = РВ + (ВС - СМ),
ЕF = АВ - АК + ВС - СМ.
С другой стороны ЕF = АК - АМ.
Сложим 2 уравнения:
2ЕF = (АВ + ВС - (АМ + СМ) = 12 + 5 - 10 = 7.
Разделим на 2: ЕF = 7/2 = 3,5.