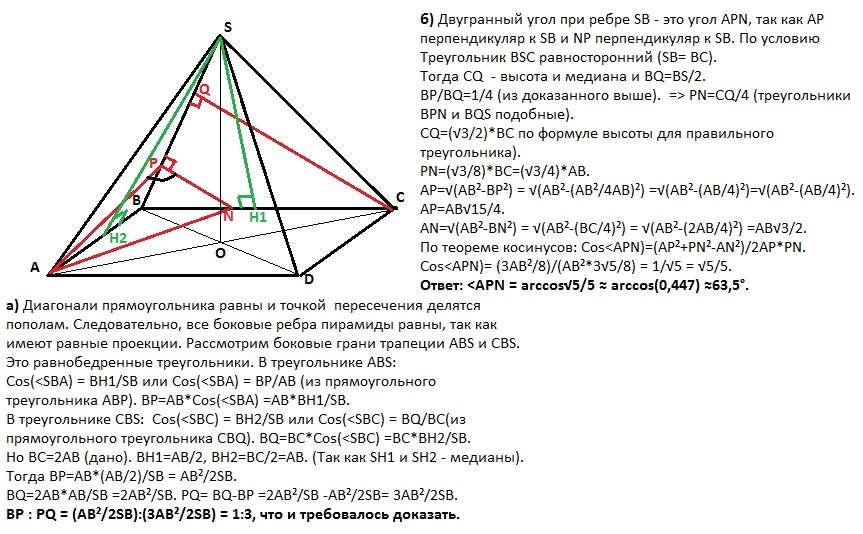
Основанием пирамиды SABCD является прямоугольник ABCD , в котором BC = 2 AB. Диагонали прямоугольника ABCD пересекаются в точке O. Отрезок SO является высотой пирамиды SABCD. Из вершин A и C опущены перпендикуляры AP и CQ на ребро SB.
а) Докажите, что BP : PQ = 1 : 3.
б) Найдите двугранный угол пирамиды при ребре SB, если SB = BC.
Ответы
а) Диагонали прямоугольника равны и точкой пересечения делятся пополам. Следовательно, все боковые ребра пирамиды равны, так как имеют равные проекции. Рассмотрим боковые грани трапеции ABS и CBS. Это равнобедренные треугольники. В треугольнике АВS:
Cos(<SBA) = BH1/SB или Cos(<SBA) = BР/АB (из прямоугольного треугольника АВР). ВР=АВ*Cos(<SBA) =АВ*ВН1/SB.
В треугольнике CВS: Cos(<SBC) = BH2/SB или Cos(<SBC) = BQ/BC(из прямоугольного треугольника CВQ). ВQ=BC*Cos(<SBC) =ВС*ВН2/SB.
Но ВС=2АВ (дано). ВН1=АВ/2, ВН2=ВС/2=АВ. (Так как SH1 и SH2 - медианы). Тогда ВР=АВ*(АВ/2)/SB = АВ²/2SB.
ВQ=2АВ*АВ/SB =2АВ²/SB. PQ= BQ-BP =2АВ²/SB -АВ²/2SB= 3AB²/2SB.
BP : PQ = (АВ²/2SB):(3AB²/2SB) = 1:3, что и требовалось доказать.
б) Проведем NP параллельно CQ. Двугранный угол при ребре SB - это угол APN, так как АР перпендикуляр к SB и NP перпендикуляр к SB. По условию Треугольник BSC равносторонний (SB= BC).
Тогда CQ - высота и медиана и BQ=BS/2.
BP/BQ=1/4 (из доказанного выше). => PN=CQ/4 (треугольники ВPN и BQS подобные).
CQ=(√3/2)*BC по формуле высоты для правильного треугольника).
PN=(√3/8)*BC=(√3/4)*AB.
АР=√(АВ²-ВР²) = √(АВ²-(АВ²/4АВ)²) =√(АВ²-(АВ/4)²)=√(АВ²-(АВ/4)²).
АР=АВ√15/4.
AN=√(АВ²-ВN²) = √(АВ²-(BC/4)²) = √(АВ²-(2AB/4)²) =AB√3/2.
По теореме косинусов: Cos<APN)=(AP²+PN²-AN²)/2AP*PN.
Cos<APN)= (3AB²/8)/(AB²*3√5/8) = 1/√5 = √5/5.
Ответ: <APN = arccos√5/5 ≈ arccos(0,447) ≈63,5°.