Tрапеция ABCD такова,что AB = 2BC = 2CD = 2DA.Точки K, L и M на BC, CD и DA соответственно таковы, что BK/KC = CL/LD = DM/MA = 2/1. Найдите угол LMK.
Ответы
AB - большее основание трапеции (параллельные основания не могут быть равны, так как получим параллелограмм и боковые стороны также будут равны).
O - середина AB. AOСD - параллелограмм (OA=CD, OA||CD) => OC=DA. Аналогично OD=BC. Трапеция составлена из трех равносторонних треугольников.
△KCL=△LDM (по двум сторонам и углу между ними; соответствующие стороны составляют равные доли от равных длин, углы равны 60°*2=120°) => KL=LM.
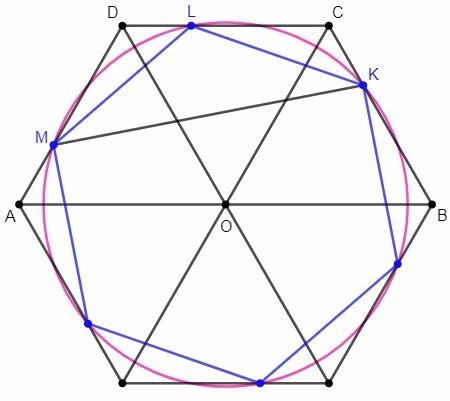
Достроим трапецию до правильного шестиугольника. На сторонах шестиугольника возьмем точки аналогично K. Получим вершины правильного шестиугольника (его стороны равны аналогично KL=LM).
Вершины правильного шестиугольника делят описанную окружности на шесть равных дуг, ∪KL=360°/6=60°.
Вписанный угол равен половине дуги, на которую опирается, ∠LMK=∪KL/2=30°.