Question

x^2-9>0 (ответ -бесконечность ,-3) но не мпогу понять почему , объясните

Answer 1

Напишу решение несколькими способами

1) Метод интервалов

x²-9>0

(x-3)(x+3)>0

___+___(-3)___-___(3)___+___

x∈(-∞; -3)U(3; +∞)

2) Разбитие на совокупность систем

x²-9>0

(x-3)(x+3)>0

Имеем произведение двух чисел, которое должно быть больше нуля. Так как "+" на "+" дает "+" и "-" на "-" дает "+"

$(x-3)(x+3)>0 \ \Leftrightarrow \ \left[\begin{array}{I} \left\{\begin{array}{I} x-3>0 \\ x+3>0 \end{array}} \\ \left\{\begin{array}{I} x-3<0 \\ x+3<0 \end{array}} \end{array}} \ \Leftrightarrow \ \left[\begin{array}{I}\left\{\begin{array}{I} x>3 \\ x>-3 \end{array}} \\ \left\{\begin{array}{I} x<3 \\ x<-3 \end{array}} \end{array}} \Leftrightarrow \ \left[\begin{array}{I} x>3 \\ x<-3 \end{array}}$

x∈(-∞; -3)U(3; +∞)

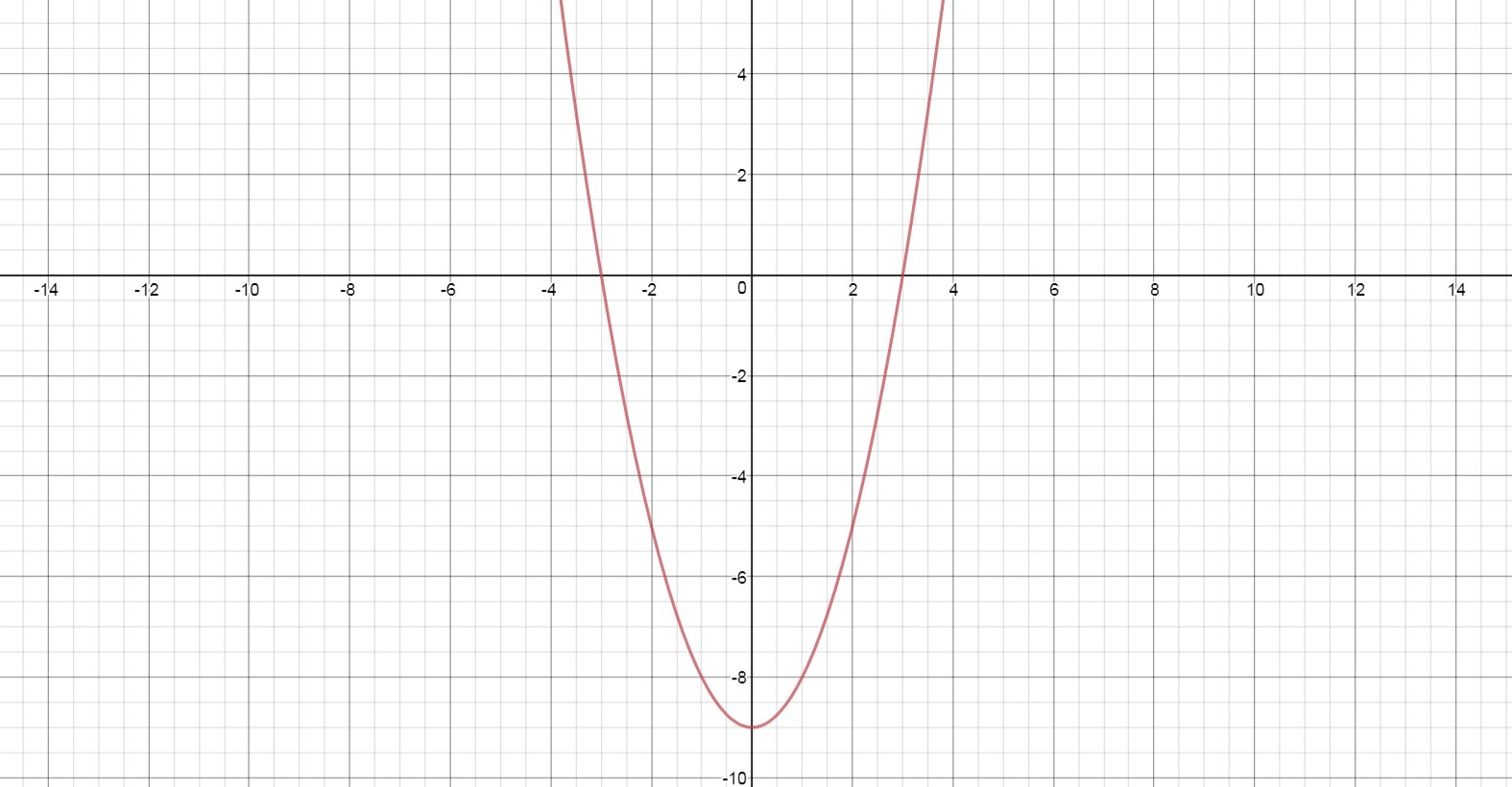
3) Графическое решение. Самое наглядное.

Строится парабола y=x²-9, после чего выбираются интервалы, где функция принимает значения больше нуля. График прикреплен.

x∈(-∞; -3)U(3; +∞)