Предмет: Алгебра,
автор: daniilscpdelta
Докажите неравенство.
Приложения:
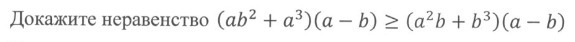
Ответы
Автор ответа:
1
Выносим за скобки два общих множителя:
Очевидно, что каждый множитель не отрицателен, значит, их произведение не отрицательно.
daniilscpdelta:
Благодарю!
Похожие вопросы
Предмет: Геометрия,
автор: mimishkakit
Предмет: Математика,
автор: soln4ko
Предмет: Математика,
автор: P2R3S5
Предмет: Физика,
автор: nosovadascha20
Предмет: Литература,
автор: милка149