Question

Найдите наибольшее значение функции
y= (4x^2-4x+4)/(4x^2-4x+3)

Answer 1

$y = \frac{4 {x}^{2} - 4x + 3 + 1}{4 {x}^{2} - 4x + 3} = 1 + \frac{1}{4 {x ^{2} - 4x + 3}}$
у(х) примет наибольшее значение, когда дробь примет наибольшее значение, а это будет, когда у1(х)=4х²-4х+3 примет наименьшее значение.
Дело в том, что у1(х)>0
Действительно,
функция у1(х) не имеет корней, т.к дискриминант
у1(х) :D=16-4*4*3<0
и раз а=4>0,
значит парабола будет вся над осью абсцисс.
то есть 4х²-4х+3>0
найдем производную:

(4х²-4х+3)'=8х-4=0
Х*=½

если не проходили производную, то можно построить параболу
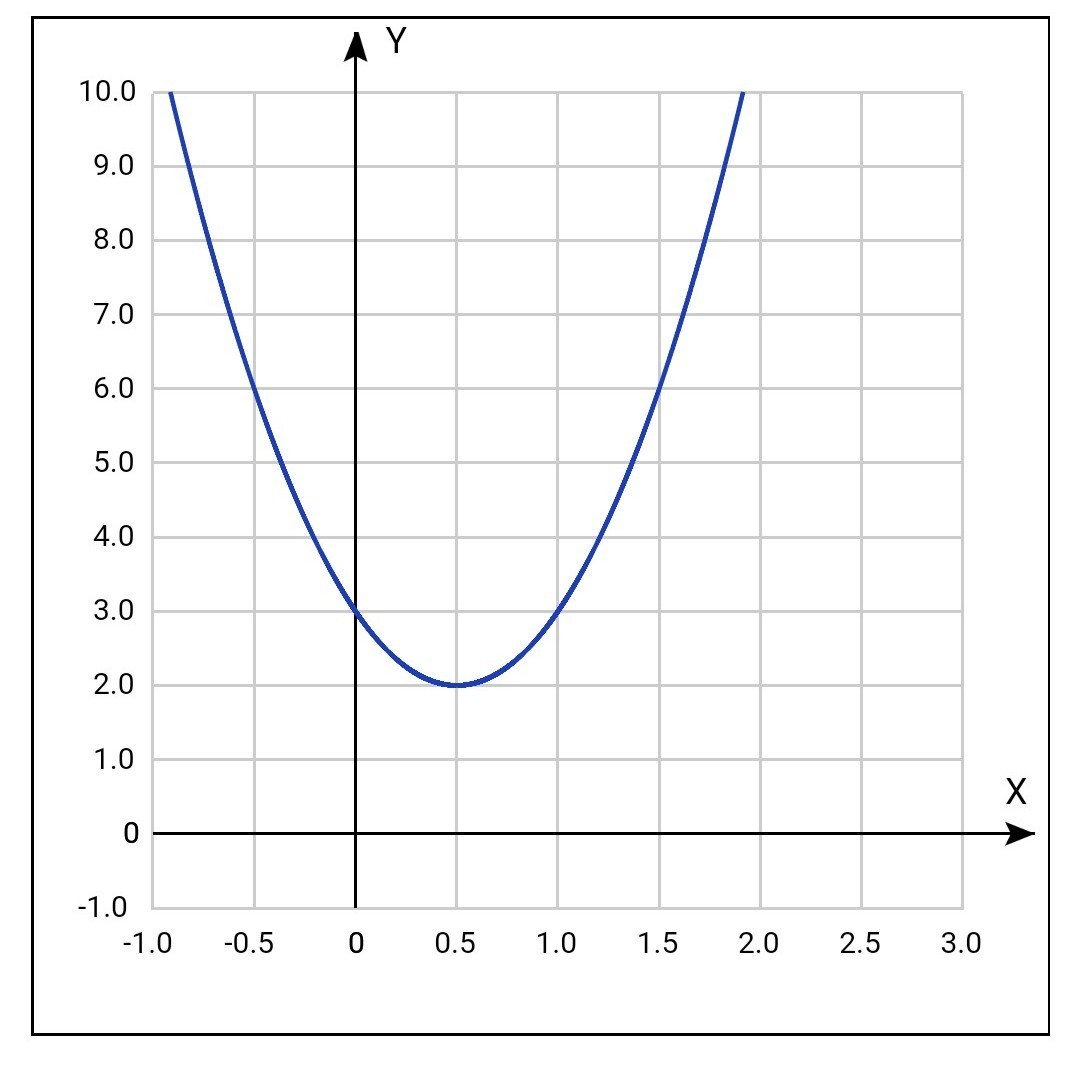
у1=4х²-4х+3 (см фото)

её вершина будет в точке
х*= -b/2a=-(-4)/(2*4)=½
и у1(х*)=2

у1 будет иметь минимум,
а наша функция
у(х)=1+( 1/у1(х))
будет иметь максимум и он равен:

f(Х*)=
=1+1/(4(1/2)²-4(1/2)+3)=1+1/(1-2+3)=1½

Ответ у наиб =1,5

Answer 2

у=(4х²-4х+4)/(4х²-4х+3)=

1+1/(4х²-4х+3)

у'=-1/(4х²-4х+3)²*(8х-4)
у'>0 функция возрастает
у'<0 функция убывает
у'=0
{8х-4=0 ;х=1/2
{4х²-4х+3≠0
Д=16-48<0
4х²-4х+3>0;х€(-оо;+оо)

у'>0;х€(1/2;+оо.)
у'<0;х€(-оо;1/2)

найдём координаты вершина
х0=4/8=1/2
у0=(48-16)/16=32/16=2

у=1+1/у0=1+1/2=3/2=1,5
у(наибольшее)=1,5