Предмет: Алгебра,
автор: yasdfasdf
Помогите пожалуйста решить показательные уравнения(неравенства)! *- это умножить. 20 баллов.

Ответы
Автор ответа:
1
4)
5)
Разделим на обе части:
6)
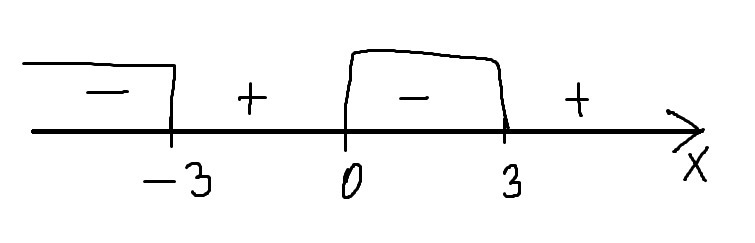
Метод декомпозиции:
или
Приложения:
Похожие вопросы
Предмет: История,
автор: olesiksmi
Предмет: Английский язык,
автор: danilarhip42
Предмет: Геометрия,
автор: stepanjalto
Предмет: Математика,
автор: настюхаверуха