Question

Решить уравнение :
Объясните, если вам не трудно
|x+1|-|x-2|+|3x+6|=5

Answer 1

подробное решение
в конце страницы написан ответ

Answer 2

постоянный положительный множитель можно выносить за знак модуля, поэтому уравнение примет вид:

|x+1|-|x-2|+3|x+2|=5

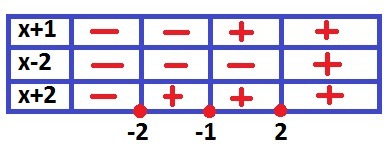
Универсальный метод решения уравнений с модулями - метод интервалов (метод расщепления)

Найдем нули подмодульных выражений:

x+1=0 => x=-1

x-2=0 => x=2

x+2=0 => x=-2

Составим небольшую таблицу, по которой определим знак каждого промежутка с помощью пробной точки (см. рисунок)

Если в промежутке стоит +, то модуль просто опускается, если же -, то знаки под модулем меняются на противоположные

1 случай)

$\left\{\begin{matrix} x<-2\\-(x+1)+(x-2)-3(x+2)=5 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x<-2\\-x-1+x-2-3x-6=5 \end{matrix}\right. \\ \\\\ \Leftrightarrow \left\{\begin{matrix} x<-2\\-3x=14 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x<-2\\x=-\frac{14}{3} \end{matrix}\right. \Leftrightarrow x=-\frac{14}{3}$

2 случай)

$\left\{\begin{matrix} -2\leq x<-1\\-(x+1)+(x-2)+3(x+2)=5 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\-x-1+x-2+3x+6=5 \end{matrix}\right. \\ \\ \\\Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\3x=2 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\x=\frac{2}{3} \end{matrix}\right. \Leftrightarrow x \in \O$

3 случай)

$\left\{\begin{matrix} -1\leq x<2\\(x+1)+(x-2)+3(x+2)=5 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\x+1+x-2+3x+6=5 \end{matrix}\right. \Leftrightarrow \\ \\ \\ \Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\5x=0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} -2\leq x<-1\\x=0 \end{matrix}\right. \Leftrightarrow x=0$

4 случай)

$\left\{\begin{matrix} x \geq 2\\(x+1)-(x-2)+3(x+2)=5 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x \geq 2\\x+1-x+2+3x+6=5 \end{matrix}\right. \Leftrightarrow \\ \\ \\ \Leftrightarrow \left\{\begin{matrix} x \geq 2\\3x= -4\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x \geq 2\\x= -\frac{4}{3}\end{matrix}\right. \Leftrightarrow x \in \O \\ \\ \\ OTBET: \ -\frac{14}{3}; \ 0$