Question

Пожалуйста помогите
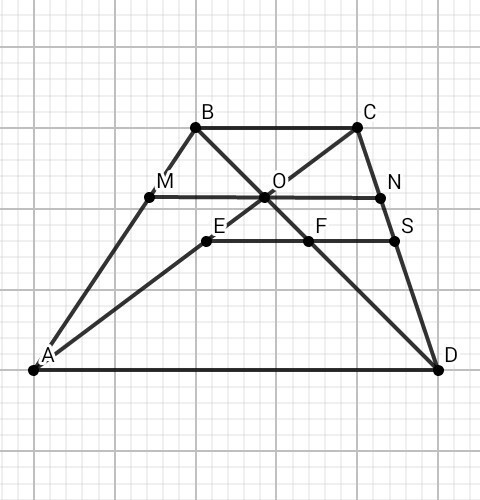
Прямая параллельная основанию AD трапеции ABCD проходит через точку пересечения диагоналей трапеции и пересекает боковые стороны в точках M и N. Известно что AD=4 и MN=3. Чему равно меньшее основание и расстояние между серединами диагоналей?

Answer 1

O - точка пересечения диагоналей.

△AOD~△COB

OD/BO=AD/BC

Параллельные отсекают от угла подобные треугольники.

△ABD~△MBO

AD/MO=BD/BO =(BO+OD)/BO = 1 +OD/BO = 1 +AD/BC <=>

1/MO= 1/AD +1/BC

Аналогично 1/ON= 1/AD +1/BC => MO=ON =MN/2 =3/2

1/BC= 1/MO -1/AD =2/3 -1/4 =5/12 <=> BC=12/5 =2,4

EG - средняя линия в △ACD, EG||AD, G - середина CD.

EG=AD/2

FG - средняя линия в △BDC, F - середина BD.

FG=BC/2

EF=EG-FG =(AD-BC)/2 =2 -1,2 =0,8

Answer 2

Решение приложено
___________________

Пусть ВС = а, AD = b, тогда
1) ∆ AOD подобен ∆ ВОС по двум углам ( ВС || AD ) → AD/BC = OD/BO = OA/CO = b/a
2) ∆ ABD подобен ∆ MBO по двум углам ( AD || MO) → AD/МО = АВ/BM = BD/BO
AD/MO = BD/BO = ( BO + OD)/BO = 1 + ( OD/BO ) = 1 + b/a = ( a + b )/a

AD/MO = ( a + b )/a → AD = b
MO = a·b/( a + b )
Аналогично через подобие треугольников получаем, что
ON = a·b/( a + b )
Значит, MN = MO + ON = 2·a·b/( a + b )

MN = MO + ON = 2·a·b/( a + b )
3 = 2·4·a/( a + 4 )
8a = 3·( a + 4 )
8a = 3a + 12
5a = 12
a = 12/5 = 2,4
Значит, ВС = 2,4

3) Рассмотрим ∆ ACD:
AE = EC, ES || AD → ES – средняя линия. Значит, ES = ( 1/2 )·AD
Рассмотрим ∆ BCD:
FS – средняя линия →
FS = ( 1/2 )·BC

EF = ES –FS = ( 1/2 )·AD – ( 1/2 )·BC = ( 1/2 )·( AD – BC )

Значит, EF = ( 1/2 )·( b – a )
EF = ( 1/2 )·( 4 – 2,4) = ( 1/2 )·1,6 = 0,8

ОТВЕТ: ВС = 2,4 ; EF = 0,8