Предмет: Алгебра,
автор: katenamatsueva
Найдите корни (корень)уравнения
Приложения:
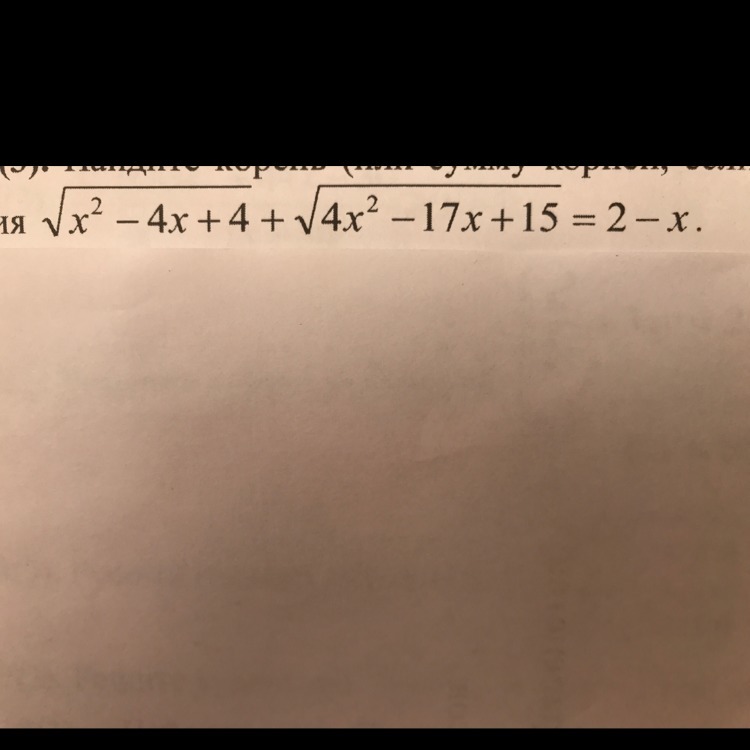
Ответы
Автор ответа:
1
Решение во вложении.
Приложения:
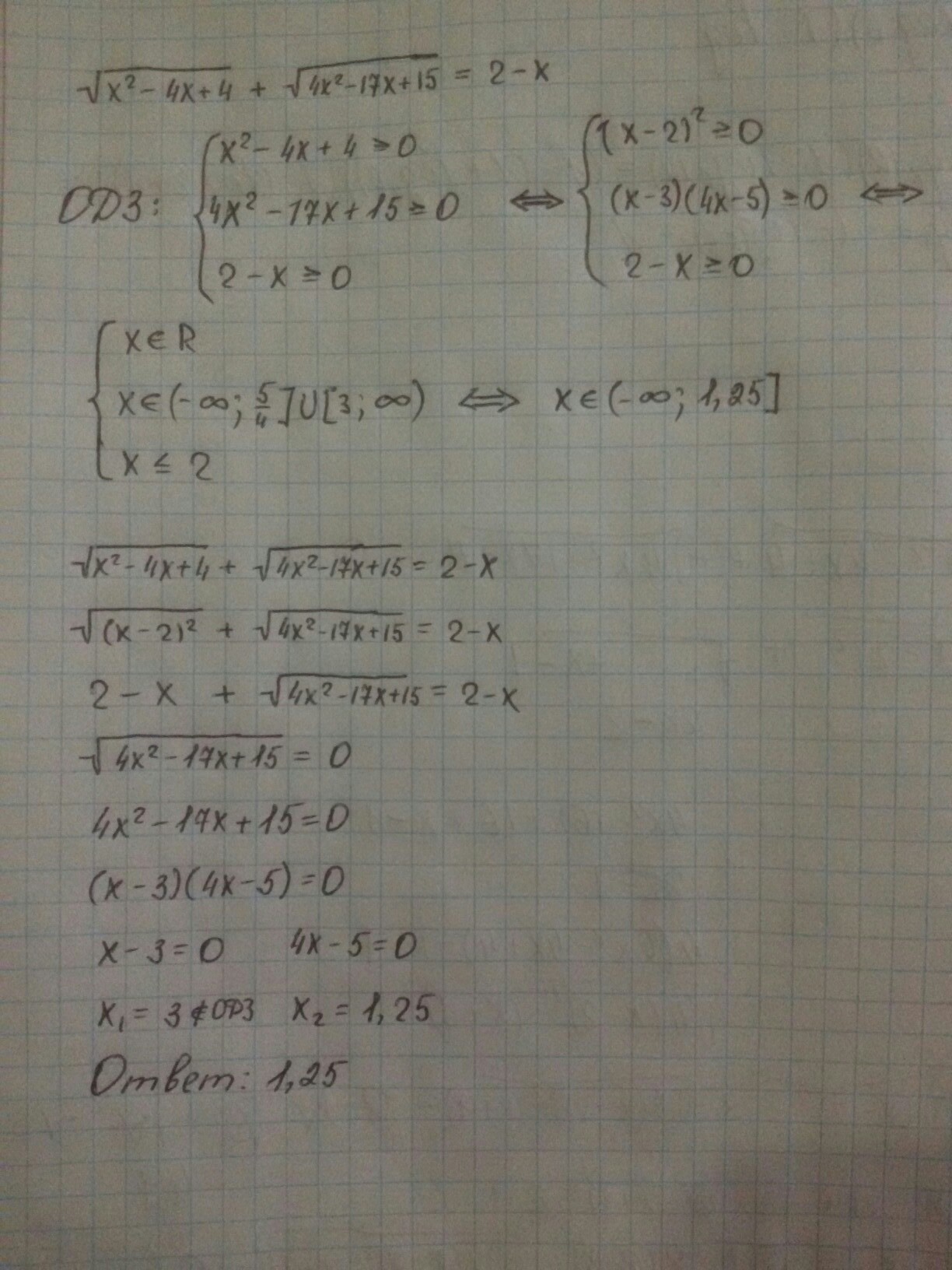
Автор ответа:
0
ОДЗ
x²-4x+4≥0
(x-2)²≥0 это будет всегда
4 x² - 17x + 15 ≥0
(x-3)(4x-5)≥0
4(x-3)(x-1,25)≥0
x≥3 и х≤1,25
2-х≥0( как сумма неотрицательных квадратных корней) или
x≤2
Поэтому ОДЗ: х≤1,25




при х≤2


х1=3 ( не подходит по ОДЗ)
х2=1,25
Случай х>2 не рассматриваем, т к эти х не входят в ОДЗ: х≤1,25
Ответ х=1,25
x²-4x+4≥0
(x-2)²≥0 это будет всегда
4 x² - 17x + 15 ≥0
(x-3)(4x-5)≥0
4(x-3)(x-1,25)≥0
x≥3 и х≤1,25
2-х≥0( как сумма неотрицательных квадратных корней) или
x≤2
Поэтому ОДЗ: х≤1,25
при х≤2
х1=3 ( не подходит по ОДЗ)
х2=1,25
Случай х>2 не рассматриваем, т к эти х не входят в ОДЗ: х≤1,25
Ответ х=1,25
Похожие вопросы
Предмет: География,
автор: S0faWwW
Предмет: Химия,
автор: sarvinozkhodzhiboeva
Предмет: Алгебра,
автор: keelmeena
Предмет: Математика,
автор: Аноним