Question

а) Решите уравнение:
$\dfrac{\sqrt{sin\ x+0,5}\cdot(0,5\cdot log_{\sqrt{7}}sin\ x\ +3\cdot log_{343}cos\ x+\dfrac{log_52}{log_57}) }{cos^26x-1}=0$
б) Укажите все корни этого уравнения из промежутка $(\ lg(cos\ 2\pi);\ e^{2ln\sqrt{2\pi}}\ ]$

Answer 1

.......................

Answer 2

а) $sinx=-0.5$ или $log_{7}sinx+log_{7}cosx+log_{7}2=0$

Из 2-го уравнения следуют ограничения: $sinx>0; cosx>0$

1-й корень отпадает, остаётся только:

$log_{7}(2sinxcosx)=0$

$2sinxcosx=1$

$sin2x=1$

$x=\frac{\pi}{4}+2\pi k$, k - целое

б) $lg(cos2\pi )=lg1=0$

$e^{2ln\sqrt{2\pi}}=(e^{ln\sqrt{2\pi})^2=2\pi$

То есть промежуток $(0; 2\pi ]$

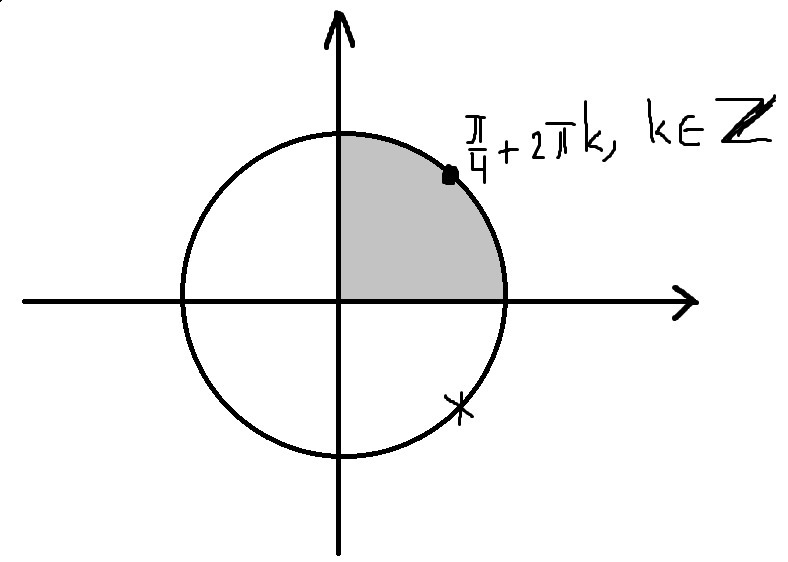
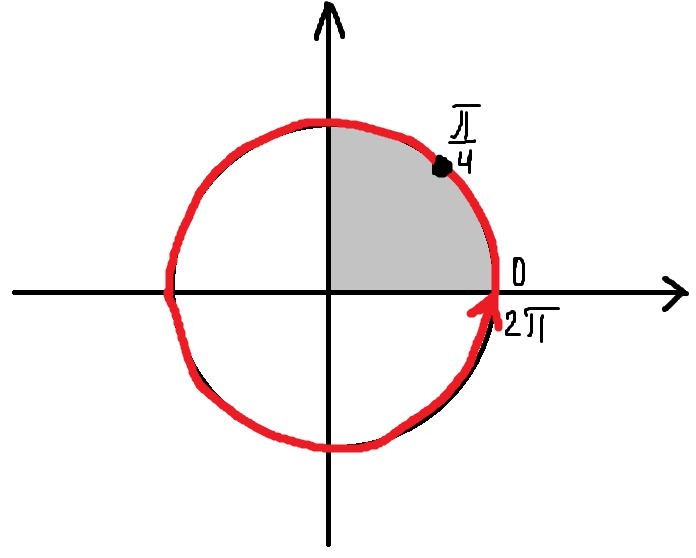
Отбор корней проведём с помощью тригонометрической окружности

Ответ: а) $\frac{\pi}{4}+2\pi k,$ k - целое; б) $\frac{\pi}{4}$

p.s. написал, потому что ничего не понял в прошлом решении