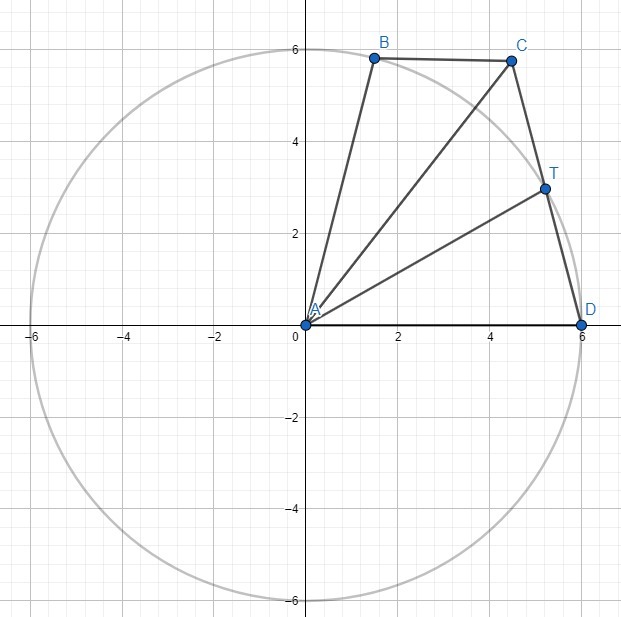
Докажите, что угол BAC равен углу CAT. Всё что нам дано: рисунок, BC=AD/2, CT=TD. На рисунке используйте лишь расположение точек, т.е. на надо писать что трапеция ABCD равнобедренная, потому что она выглядит как равнобедренная, хотя она действительно равнобедренная, но это нужно доказать)
Ответы
1. Проведем среднюю линию трапеции ТМ, которая пересечет диагональ трапеции AC в точке Q. Рассмотрим треугольник АМТ. В нем сторона АМ=AB/2 = R/2 (так как МТ - средняя линия трапеции). Сторона АТ=R. Следовательно, АМ/АТ = (R/2)/R = 1/2.
МQ=BC/2 (так как MQ - средняя линия треугольника АВС).
QT=AD/2=BC/4 (средняя линия треугольника АСD. Тогда MQ/QT=(BC/2)/(BC/4)=1/2.
Отрезок AQ является биссектрисой угла АМТ по свойству биссектрисы: "биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам". В нашем случае: АМ/АТ=MQ/QT => AQ - биссектриса угла АМТ.
Следовательно, <BAC=<CAT, что и требовалось доказать.
2. Треугольники АВС и АСТ равны по двум сторонам и углу между ними (<BAC=<CAT - доказано выше, АВ=АТ - радиусы, АМ - общая). => ВС=СТ. => CD=AD (так как CD и AD равны 2*ВС). АВ=AD как радиусы. => AB=CD, то есть трапеция ABCD равнобедренная, что и требовалось доказать.
