Предмет: Математика,
автор: mleosevich
Помогите пожалуйста!!!!!
Приложения:
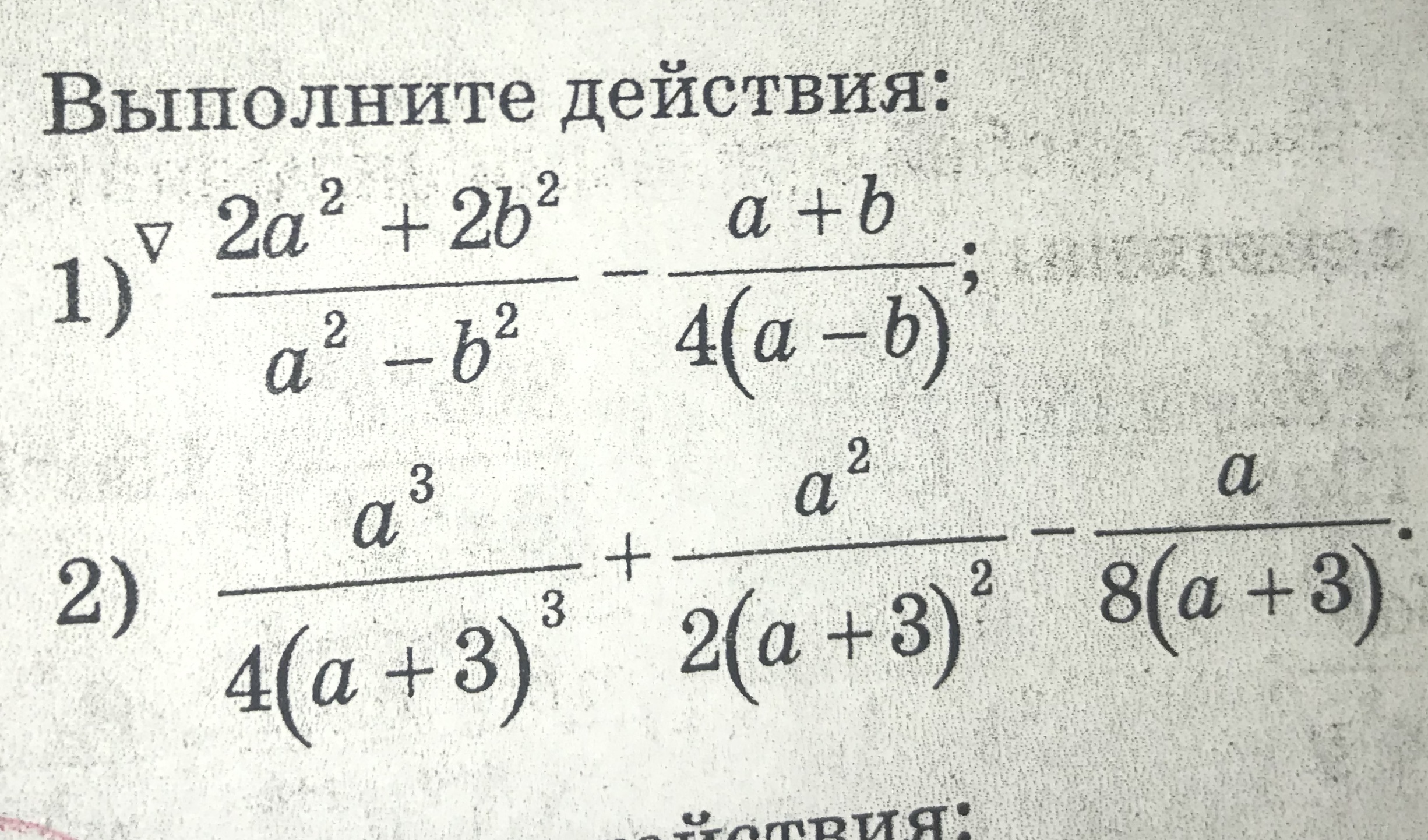
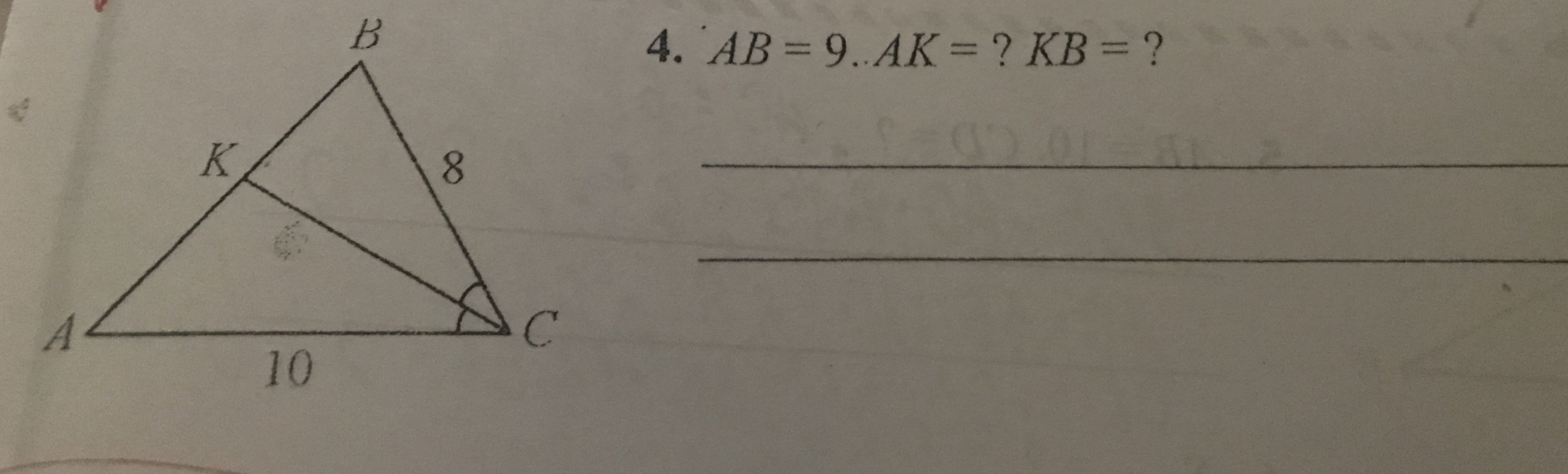
Ответы
Автор ответа:
0
1. Выполните действия:
Приведём к общему знаменателю дроби и упростим числитель:
1)
2)
2. Задача.
Дано: ABC - треугольник, AB = 9, BC = 8, AC = 10; CK - биссектриса.
Найти: AK - ? KB - ?
Решение. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла: , где
. Отсюда
Определим длину отрезка АК:
Следовательно, длина отрезка КВ равна:
Ответ: АК = 5; КВ = 4.
Похожие вопросы
Предмет: Математика,
автор: iejdjdkdk
Предмет: Другие предметы,
автор: lilichkakalinina
Предмет: Биология,
автор: rubengrigoran56
Предмет: Физика,
автор: Gogol2020