Question

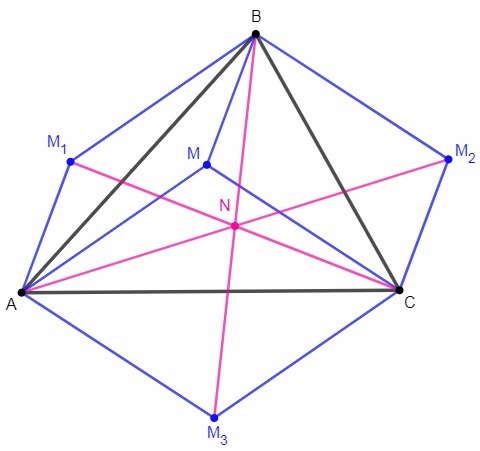
Внутри треугольника АВС взята точка М и построены параллелограммы АМВМ1, ВМСМ2 и СМАМ3. Докажите, что прямые АМ2, ВМ3 и СМ1 пересекаются в одной точке. Помогите пожалуйста.

Answer 1

Противоположные стороны параллелограмма равны и параллельны.

AM1||BM, BM||CM2 => AM1||CM2

AM1=BM, BM=CM2 => AM1=CM2

ACM2M1 - параллелограмм (противоположные стороны равны и параллельны).

N - середина AM2 и CM1 (диагонали параллелограмма точкой пересечения делятся пополам).

Аналогично ABM2M3 - параллелограмм, N - середина AM2 и BM3.

Точка N является общей серединой отрезков AM2, BM3, CM1.