Предмет: Алгебра,
автор: kisonix
Решить уравнение.....
Приложения:
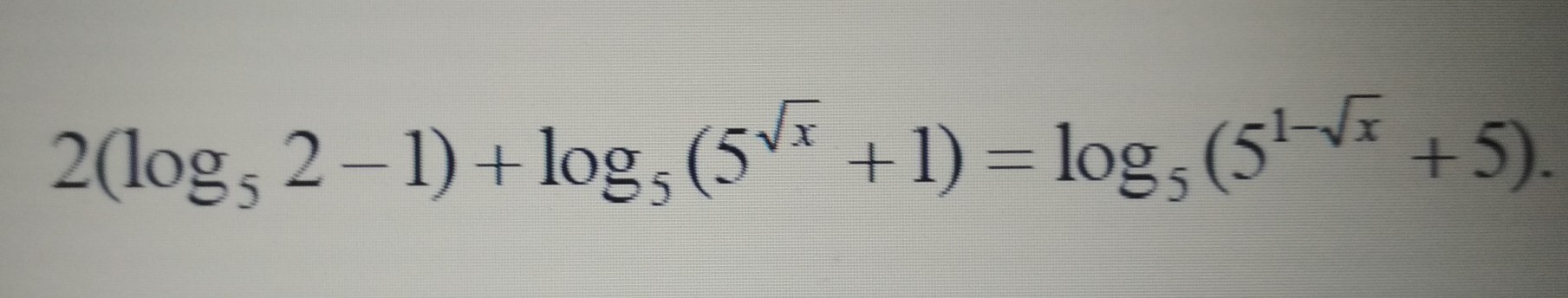
Ответы
Автор ответа:
1
kisonix:
и у меня так вышло, но в ответах 9
Ошибка в ответе
вот и я так думаю
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Биология,
автор: vewixyqi
Предмет: Окружающий мир,
автор: Maga00037
Предмет: Информатика,
автор: alinailiasovna