Предмет: Алгебра,
автор: kuzyaev01
РЕШИТЕ НЕРАВЕНСТВО CРОЧНО КАК МОЖНО СКОРЕЕ ПОЖАЛУЙСТА МНЕ УЖЕ НАДОЕЛО ЖДАТЬ КОГДА ОТВЕТЯТ 
LFP:
чтобы не ждать, нужно самому решать))
вот это решение блин
это не решение... это комментарий))
знаю
Ответы
Автор ответа:
1
x∈[0; 1)U(2;3]
Приложения:
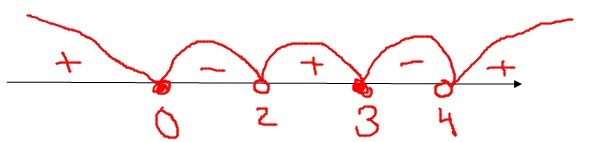
только на рисунок "не те" точки попали...
та да
Для заказчика: на рисунок наносим точки (вместо тех, что у меня) 0, 1, 2, 3
Похожие вопросы
Предмет: Физика,
автор: zopa123456
Предмет: Геометрия,
автор: karinaguza42
Предмет: Английский язык,
автор: rolariga209
Предмет: Математика,
автор: maratyapscheva
Предмет: Алгебра,
автор: Yudina2002Vika