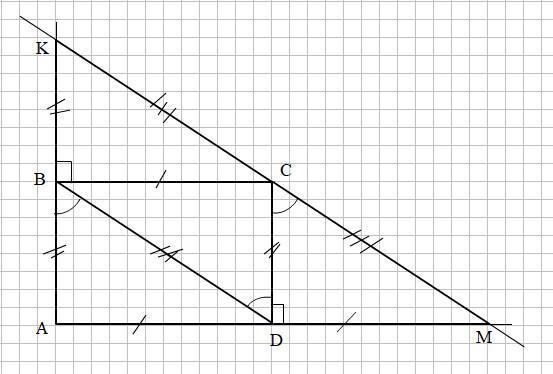
Через вершину С прямоугольника ABCD проведена прямая, параллельная диагонали BD, которая пересекает прямые AB и AD в точках K и M соответственно. Найдите длину отрезка KM, если диагональ AC равна 6 см.
Ответы
Ответ:
KM = 12см
Объяснение:
Смотри рисунок на прикреплённом фото
BD = АС = 6cм - диагонали прямоугольника.
ВС = АD и АВ = CD (противоположные стороны прямоугольника)
∠ABD = ∠BDC как накрест лежащие при АВ ║ CD и секущей BD.
∠BDC = ∠DCM как накрест лежащие при BD║ CM и секущей CD.
Тогда ∠ АВD = ∠BDC = ∠ DCM.
ΔABD = Δ DCM по катету (АВ = CD) и прилежащему к катету углу (∠ АВD = ∠DCM).
Тогда в равных треугольниках равны и другие катеты AD = DM, а также гипотенузы СМ = BD = 6см.
По теореме Фалеса: если АD = DM, то и ВК = АВ как отрезки, отсекаемые параллельными прямыми BD и KM на сторонах угла КАМ.
ΔАВD = ΔBKC по двум катетам AB = BK и AD = BC. Следовательно, равны и гипотенузы этих треугольников: КС = BD = 6cм.
Итак, КС = СМ = BD = 6cм
КМ = КС + СМ = 6см + 6см = 12см