Question

Помогите пожалуйста с параметрами срочно

Answer 1

1) $(\sqrt{4x-x^2})^4-32\sqrt{4x-x^2}=a^2-14a$

$f'(\sqrt{4x-x^2})=4(\sqrt{4x-x^2})^3-32=4((\sqrt{4x-x^2})^3-8)=0$

$\sqrt{4x-x^2}=2$

В точке 2 левое выражение равно -48. То есть

$-48\leq (4x-x^2)^2-32\sqrt{4x-x^2}\leq 0$

То есть $-48\leq a^2-14a \leq 0$

$0\leq a\leq 6$ или $8\leq a\leq 14$

Ответ: [0; 6] ∪ [8; 14]

2) 1-е уравнение задаёт пару окружностей, с центрами $O_{1}(-5;4)$ и $O_{2}(5;4)$ и радиусом 2

2-е уравнение задаёт окружность с центром в точке $A(2;0)$ и радиусом $\sqrt{a}$.

Пусть $O_{1}$ центр окружности $w_{1}$, а $O_{2}$ - центр окружности $w_{2}$. $A$ - центр окружности $z$

Заметим, что окружность $z$ ближе к $w_{2}$, чем к $w_{1}$

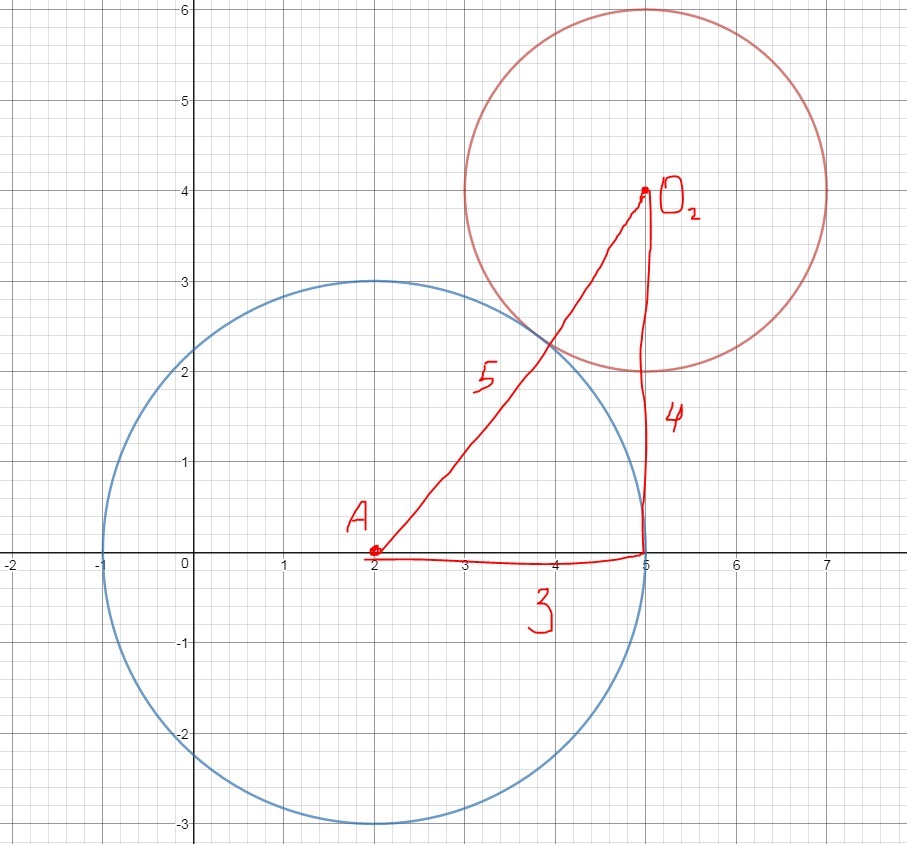
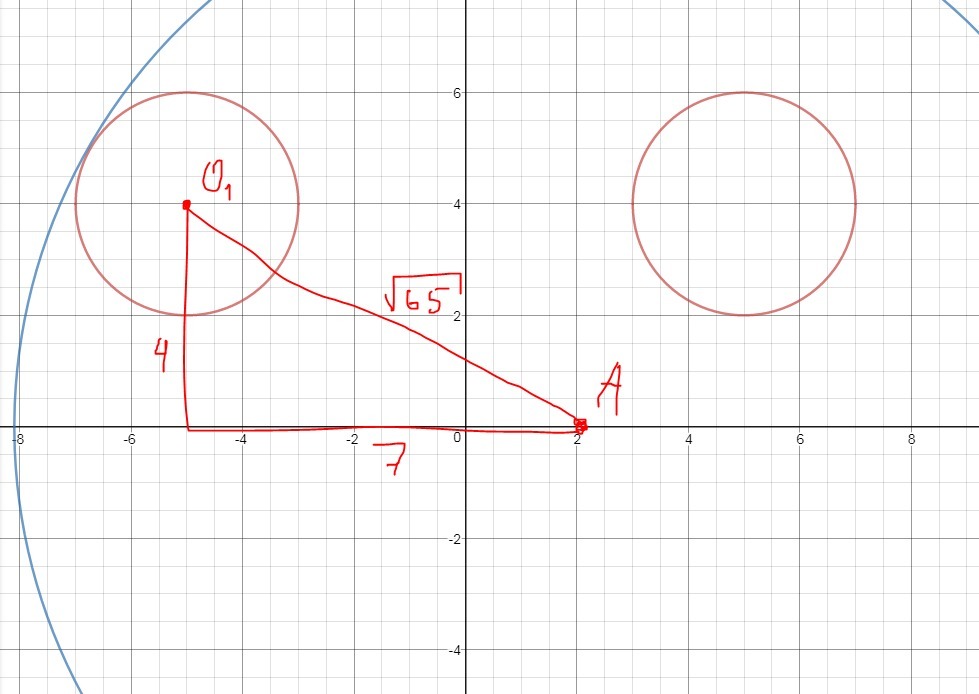
Единственное решение будет при касании $w_{2}$ внешним образом и касании $w_{1}$ внутренним образом.

1-ю точку легко находим: $a=5-2=3$ - египетский треугольник (рис.1)

2-ю точку тоже: $\sqrt{65}+2$

Ответ: $a=3; a=\sqrt{65}+2$