Question

З точки кола до діаметра проведено перпендикуляр 24 см який ділиьб діаметр на відрізка що відносяться як 9:4 занйти довжину кола

Answer 1

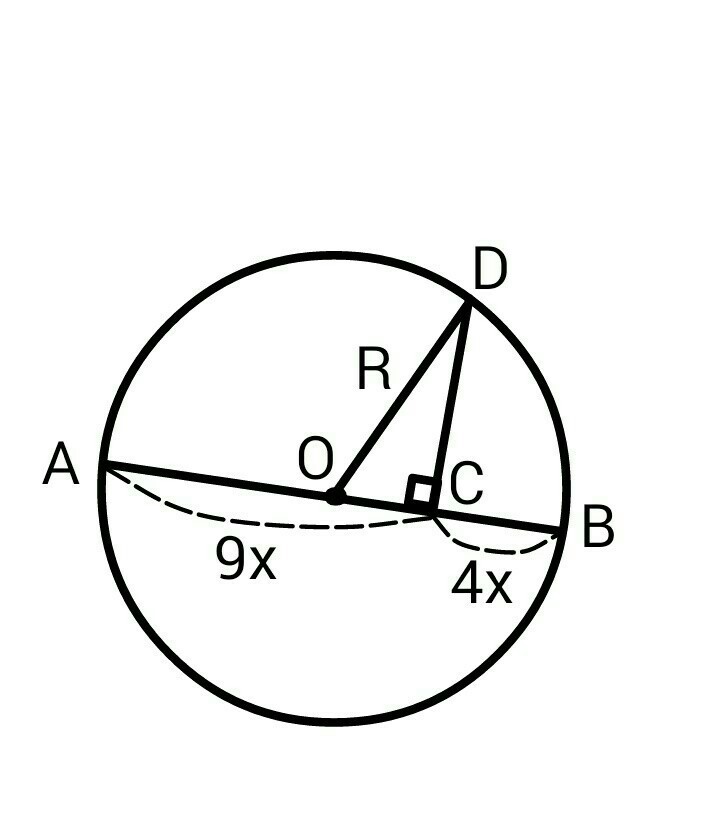
CD = 24 см
AB - диаметр.
АВ = 9х + 4х = 13х
R - радиус.
R = OD = AB/2 = 13x/2 = 6.5x
OC = 9x - R = 9x - 6.5x = 2.5x
По теореме Пифагора:
OD² = OC² + CD²
6.5²x² = 2.5²x² + 24²
42.25х² = 6.25х² + 24²
36х² = 24²
6х = 24
х = 4
R = 6.5x = 6.5*4 = 26 см
L - длинна окружности.
L = 2*π*R = 2*3.14*26 = 163.28 см
Ответ: длинна окружности L = 163.28 см

Answer 2

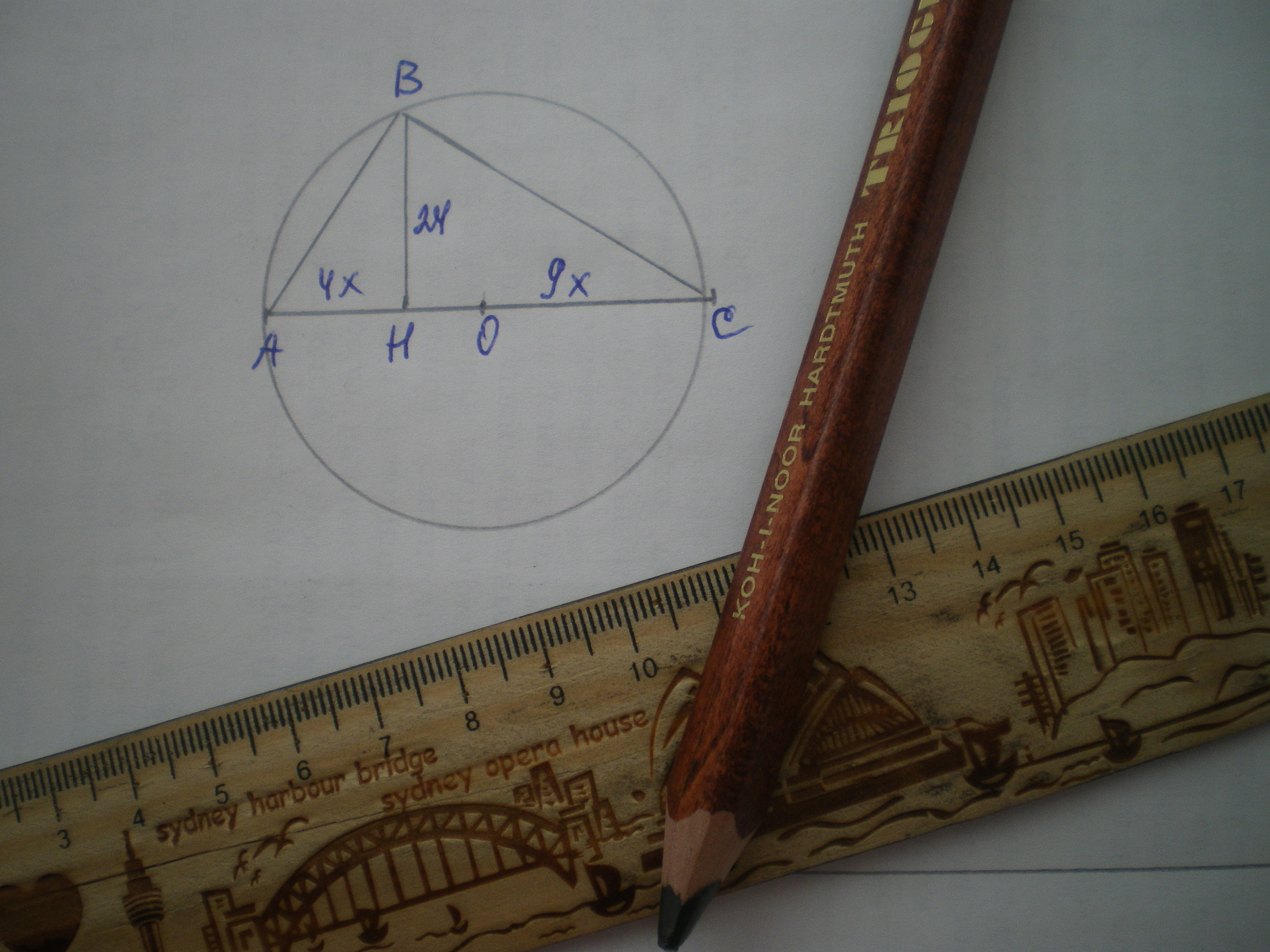
Дано: коло; АС - діаметр; ВН⊥АС; ВН=24 см; АН:СН=4:9.

Знайти довжину кола.

На діаметр кола спирається прямий кут, тому ΔАВС - прямокутний, ∠В=90°. Використаємо властивість висоти прямокутного трикутника, проведеної до гіпотенузи: ВН²=4х*9х; 576=36х²; х²=16; х=4.

АН=4*4=16 см; СН=9*4=36 см; АС=16+36=52 см. R=АО=ОС=52:2=26 см.

Довжина кола с=2πR=2π*26=52π см.