Предмет: Алгебра, автор: kisonix

Решить уравнение.......

Приложения:

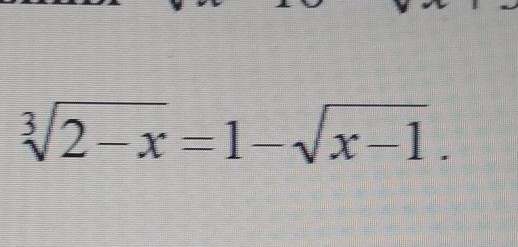
NeZeRAvix: в куб возвести и все решается

NeZeRAvix: x=1, x=2, x=10

kisonix: значит, я где-то затупила, потому что зашла в тупик. спасибо

Ответы

Автор ответа: NeZeRAvix

$\sqrt[3]{2-x}=1-\sqrt{x-1}$

Возводим в куб

$2-x=1-3\sqrt{x-1}+3x-3-(x-1)\sqrt{x-1}\\ 4-4x=-\sqrt{x-1}(x+2)\\ -4(x-1)+\sqrt{x-1}(x+2)=0\\ \sqrt{x-1}(-4\sqrt{x-1} +x+2)=0\\ \\ \sqrt{x-1}=0\\ x-1=0\\ x=1\\ \\ x+2=4\sqrt{x-1}\\ x^2+4x+4=16x-16\\ x^2-12x+20=0\\ \frac{D}{4}=36-20=16=4^2\\ x_1=6-4=2\\ x_2=6+4=10$

Проверка на посторонние корни:

$\sqrt[3]{2-1}=1-\sqrt{1-1}\\ 1=1\\ \\ \sqrt[3]{2-2}=1-\sqrt{2-1}\\ 0=0\\ \\ \sqrt[3]{2-10}=1-\sqrt{10-1} \\ -2=-2$

Ответ: 1; 2; 10

999Dmitry999: Я вам такие же корни найду на графики.

xERISx: На графике можно найти корни с некоторой точностью, либо с попаданием в интервал. Вычислить на графике корень, бесконечно приближающийся к некоторому числу, невозможно. Любой иррациональный корень будет представлен конечной дробью. Графический способ может облегчить поиск корней, но не может заменить точные вычисления.

999Dmitry999: В данном случае ,если построить график ,то моно сразу увидеть корни и там нет такого корня ,которого мы бы не нашли (в этом примере)

NeZeRAvix: Напомнило решение в лоб, потому что оно в лоб

xERISx: Дмитрий, а вы сможете дать гарантию, не вычисляя, что корень х=1, а не х=0,(9)?

999Dmitry999: Да. Смогу. Возьму две функции и начну с левой ,точки писать не буду ,но вот как выглядит этот график мы с вами знаем хорошо) Парабола которая упала ,да и без половины ,но так называемая вершина начинается по x=1,а когда будем строить вторую функцию ,то увидим пересечение. Я говорю ,что графический метод тут и именно ту хорошо подходит.Я не говорил и не хотел сказать :"Бросьте аналитические методы и решайте графическими способами",нет! Тут он хорошо подходит ,а там нет)

NeZeRAvix: Конкретно в этом уравнении корни целые, поэтому графический метод может быть и уместен, однако если бы корни были, например, (3±√5)/2, у вас бы получилось только приблизительное значение. Нельзя же ведь знать, что корни целые заранее?

999Dmitry999: Нельзя. Я и уточняю ,что в именно в этом уравнении можно воспользоваться графическим методом. Я ПОПРОБОВАЛ и получил корни (хорошие) .Почему бы просто не попробовать)))

NeZeRAvix: Ну, 10 раз попробуете, 9 раз не получится, и больше пробовать не будете)

999Dmitry999: Спасибо за мотивацию ))

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Литература, автор: Dghdbdv

ПОМОГИТЕ ПЖ СРОЧНО!!!

6 лет назад

Предмет: Русский язык, автор: bebranos123

Укажи слово, которое не является однокоренным среди данной группы:

а) кора б) корка в) покорить г) корочка ОТВЕТЬТЕ ПЖ ДАМ 15 БАЛЛОВ
Сори больше нету

6 лет назад

Предмет: Другие предметы, автор: safimalahova