Предмет: Математика,
автор: nikita67htnikita67ht
Найти производные функций
Приложения:
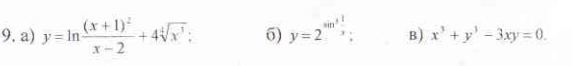
NNNLLL54:
в п. б) sin в какой степени?
Я считаю, что во 2-й.
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: s87075637419
Предмет: Математика,
автор: nurajkasieva4
Предмет: Английский язык,
автор: sashumbamedveshumba
Предмет: Биология,
автор: Аноним
Предмет: Литература,
автор: bossizhan