Предмет: Алгебра,
автор: Nishinoyaa
Решите тригонометрическое уравнение:
Sin5x-sin3x=cos4x
Ответы
Автор ответа:
2
sin5x - sin3x = cos4x
Воспользуемся формулой разности синусов:
2*sin[(5x - 3x)/2]*cos[(5x + 3x)/2] = cos4x
2sinx*cos4x = cos4x
2sinx*cos4x - cos4x = 0
cos4x(2sinx - 1) = 0
cos4x = 0 или 2sinx - 1 = 0
cos4x = 0 или sinx = 1/2
4x = π/2 + πn, n ∈ Z; x = (-1)ⁿπ/6 + πn, n ∈ Z
x = π/8 + πn/4, n ∈ Z; (-1)ⁿπ/6 + πn, n ∈ Z
Ответ: x = π/8 + πn/4; (-1)ⁿπ/6 + πn, n ∈ Z.
Автор ответа:
2
Решение (см. изображение)
Приложения:
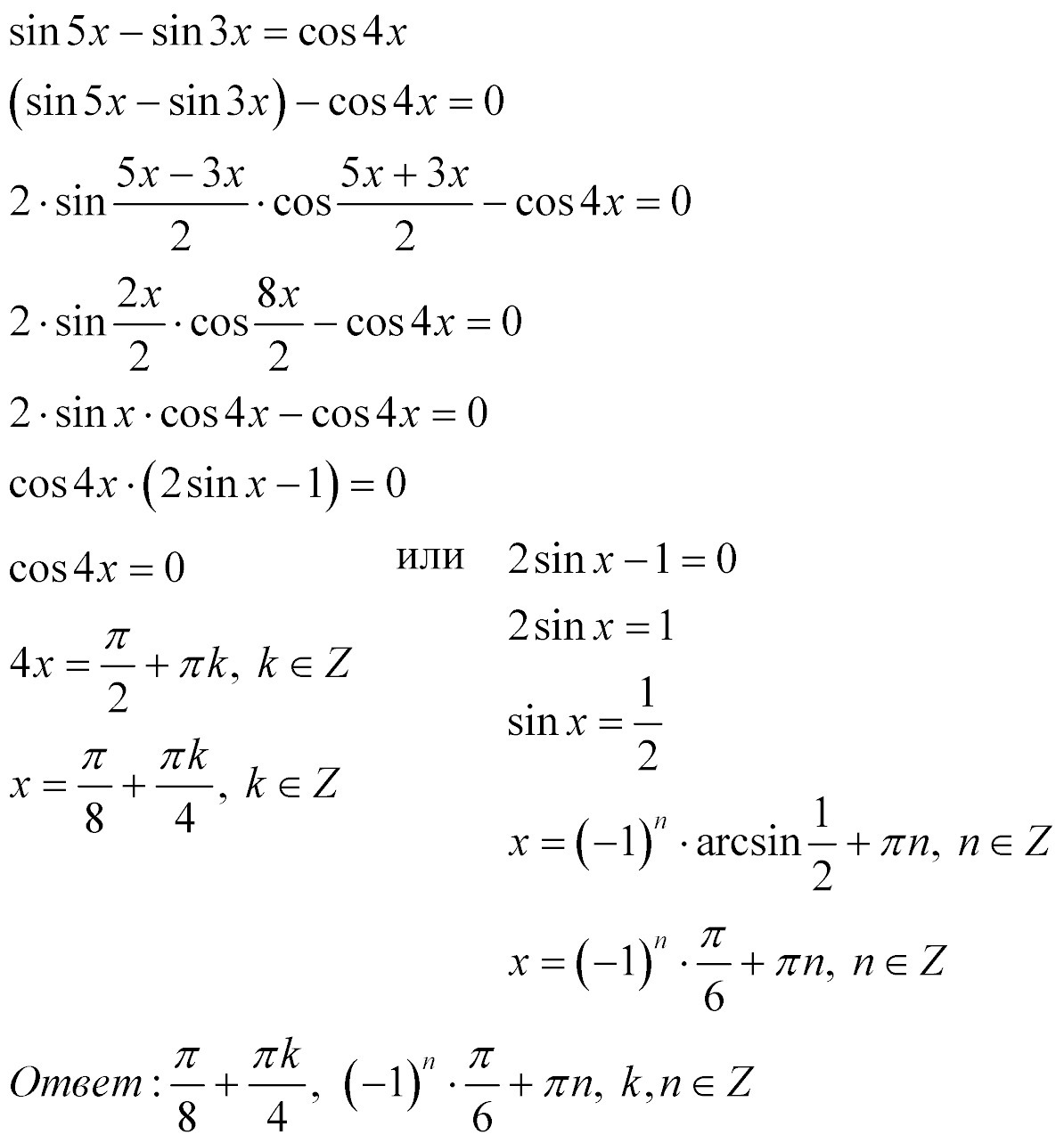
Похожие вопросы
Предмет: Математика,
автор: okimetshyryn
Предмет: Русский язык,
автор: kasietagis
Предмет: Физика,
автор: nikolaentsevartem
Предмет: Математика,
автор: ВикаВикаЧумадан