Предмет: Математика,
автор: krylovairisha9
Найдите произведение всех значений параметра а , при которых уравнение имеет единственное решение.
варианты ответов:
а)9 б) 128 в) -36 г) -96 д) корень из 10
Приложения:
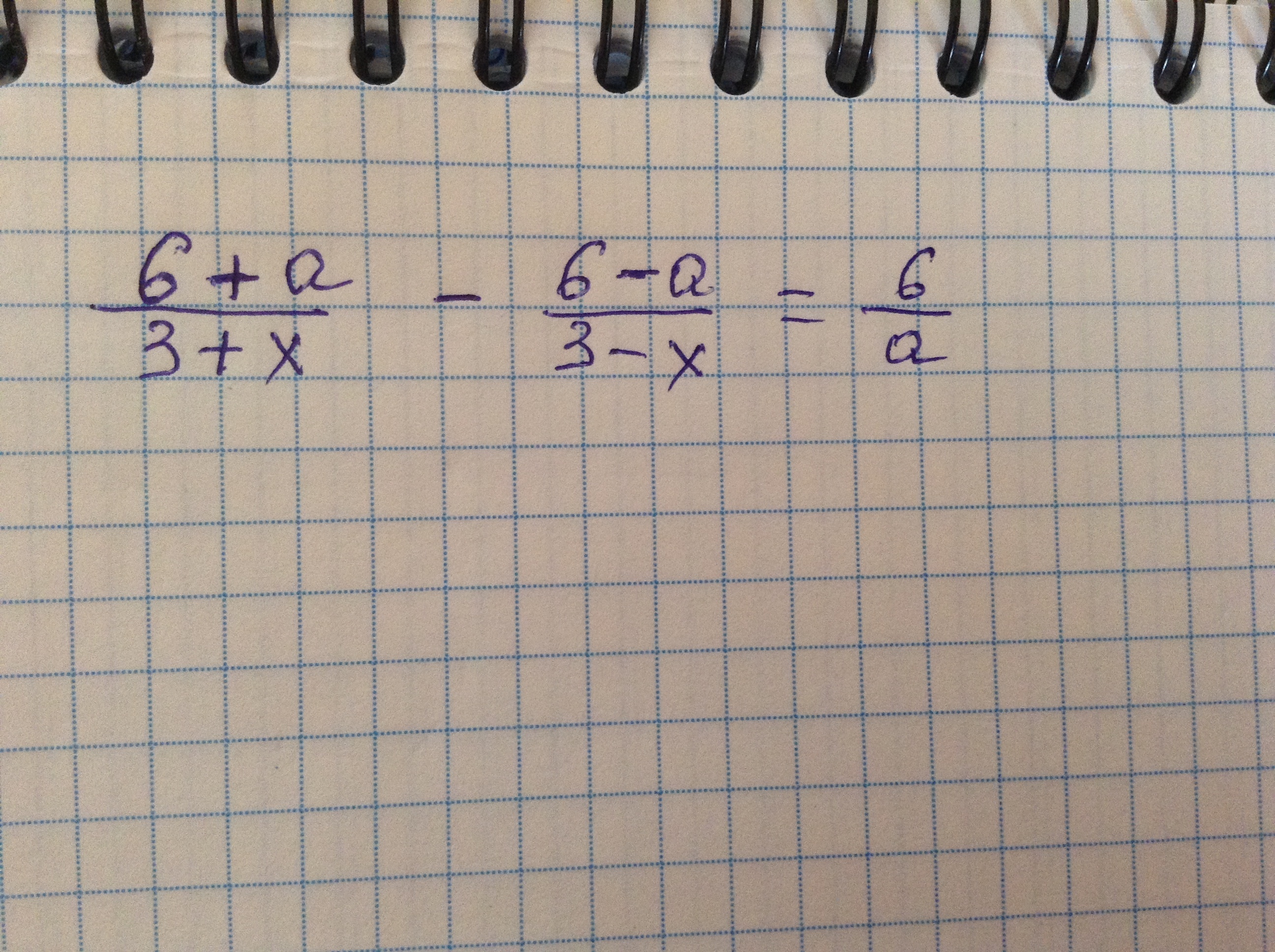
Ответы
Автор ответа:
1
Умножаем обе части уравнения на
Произведение корней по теореме Виета:
Корни: ,
Также ОДЗ:
Решим аналитически. Получилось 2 корня, а нужен 1. Значит какой-то корень должен "выпасть". Это когда 1 корень стал равен
:
- не подходит
:
- подходит
:
- подходит
:
- не подходит
Автор ответа:
1
Умножим на(3+x)(3-x)a :
18a + 3a²- 6ax - a²x - 18a + 3a²- 6ax + a²x = 54 - 6x² ;
x² - 2ax + a² - 9 = 0.
Уравнение будет иметь 1 решение, если дискриминант будет равен 0.
Д = 4а² - 4*(а² - 9) = 36.
Значит при любом значении а уравнение будет иметь 2 решения.
Похожие вопросы
Предмет: Математика,
автор: kucerlera334
Предмет: Математика,
автор: mikazajkina
Предмет: Математика,
автор: alimovatolstikh
Предмет: Математика,
автор: 8YmНиK8
Предмет: Алгебра,
автор: boogymm