Предмет: Алгебра,
автор: Веточка200
Помогите с выполнением заданий 16,17,18. Спасибо.
Приложения:

Ответы
Автор ответа:
1
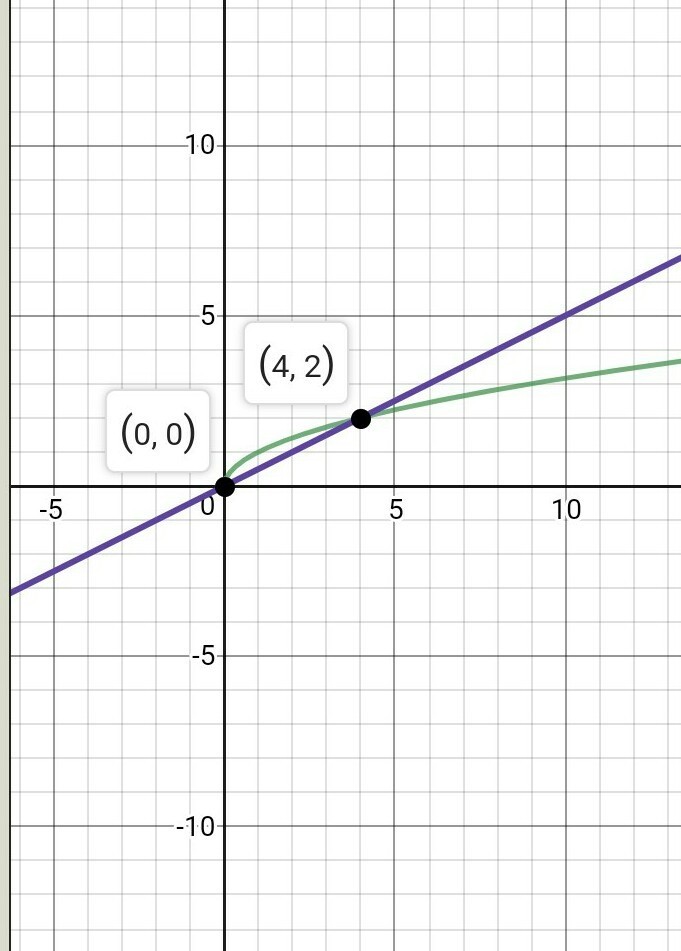
16)

Найдем некоторые точки функции:
х = 0, у = 0
x = 1, y = 1
x = 4, y = 2
Найдем некоторые точки прямой x - 2y = 0:
х = 0, у = 0
х = 4, у = 2
Графики во вложении.
Ответ: (0;0), (4; 2)
17)

18)

Найдем некоторые точки функции:
х = 0, у = 0
x = 1, y = 1
x = 4, y = 2
Найдем некоторые точки прямой x - 2y = 0:
х = 0, у = 0
х = 4, у = 2
Графики во вложении.
Ответ: (0;0), (4; 2)
17)
18)
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: MoneyMyLoveHAHAHAHA
Предмет: Другие предметы,
автор: semenovaanna866
Предмет: Биология,
автор: germanok1981a
Предмет: Математика,
автор: Lermonchik
Предмет: Алгебра,
автор: anna24011984