Предмет: Математика,
автор: potterswife
математика логарифм на фото
Приложения:
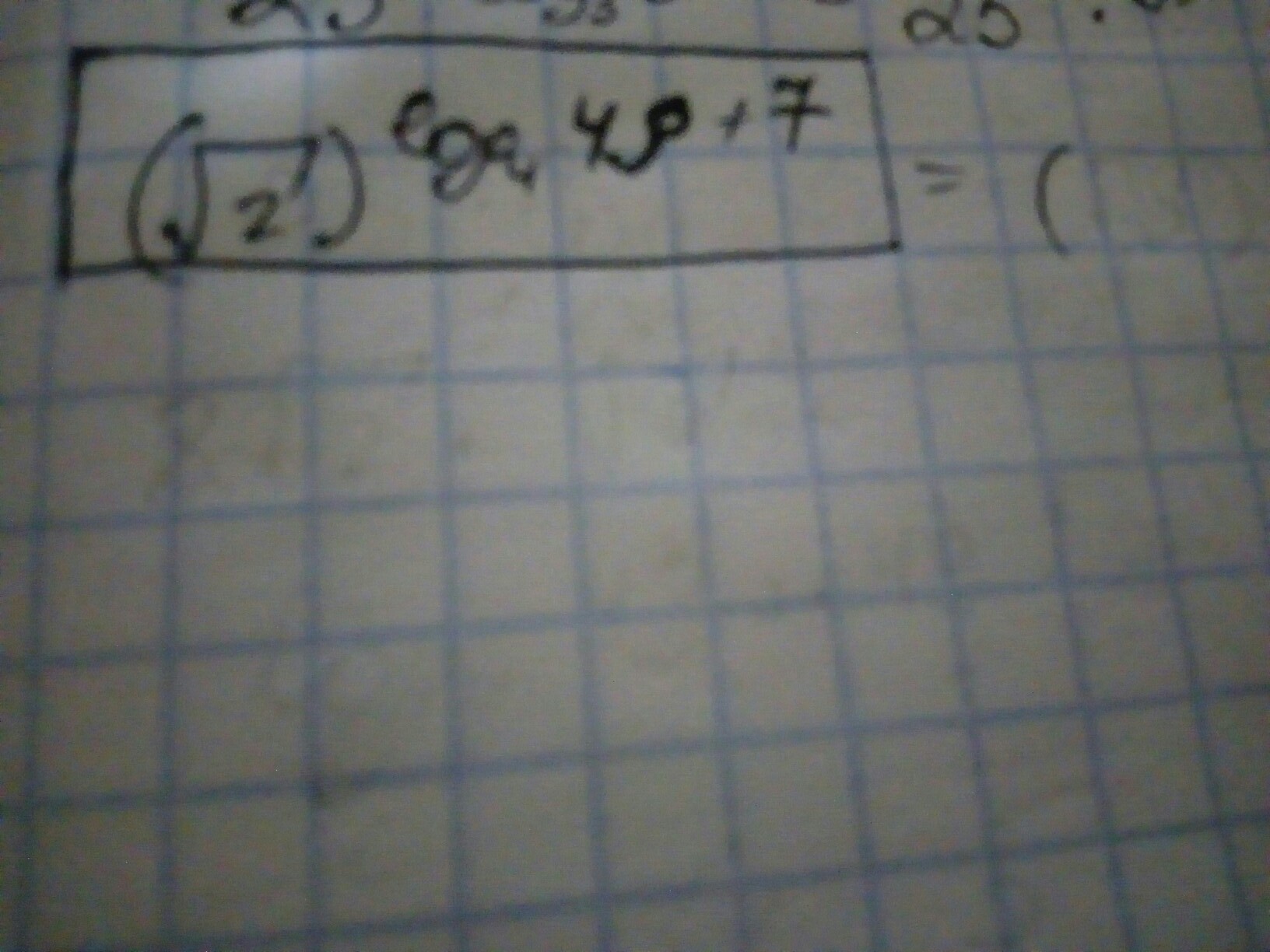
Ответы
Автор ответа:
0
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: pabramova162
Предмет: Математика,
автор: shrashenova
Предмет: Геометрия,
автор: igromanplaykipllz
Предмет: Математика,
автор: shurik0110
Предмет: Алгебра,
автор: akhunovajamilya