Основи трапеції дорівнюють 7 см і 21 см. Знайдіть бічні сторони трапеції, якщо радіус вписаного кола дорівнює 6 см.
Ответы
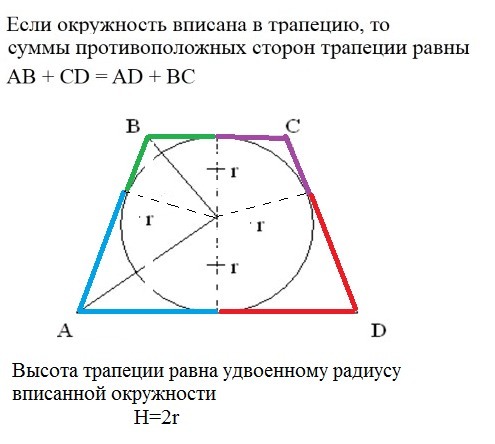
высота трапеции = 2*r = 12
если в 4-угольник можно вписать окружность, то суммы длин противоположных сторон должны быть равны.
21+7 = х+у
если провести две высоты трапеции и записать т.Пифагора для двух получившихся прямоугольных треугольников, получим систему из трех уравнений с тремя неизвестными...
Боковые стороны трапеции: 13 и 15

AB+CD=BC+AD=7+21=28.
Итак, в трапеции известны основания, высота и сумма боковых сторон.
Проводим BK || CD ( cм. рис.2)
Рассматриваем Δ АВК
AK=AD-KD=21-7=14
Проводим высоту BM=2r=12
Обозначаем АВ=х, BK=CD=28-x
По теореме Пифагора из прямоугольного треугольника ABM
АM²=AB²-BM²=x²-12²
По теореме Пифагора из прямоугольного треугольника BMK
MK²=BK²-BM²=(x-28)²-12²
АМ+МК=АКУравнение
√(х²-12²)+√((28-x)²-12²)=14;
√((28-x)²-12²)=14-√(х²-12²)
Возводим в квадрат и упрощаем
√(х²-12²) = 21 - 2х
Возводим в квадрат
x²-144=441-84x+4x²
3x²-84x+585=0
D=84²-4·3·585=4·(4·441-3·585)=4·9=6²
x=(84-6)/6=13 или (84+6)/6=15
Cоответственно вторая сторона 15 или 13
О т в е т. 13 и 15