Предмет: Алгебра,
автор: Tankist57
Решите пожалуйста;) буду благодарен
Приложения:
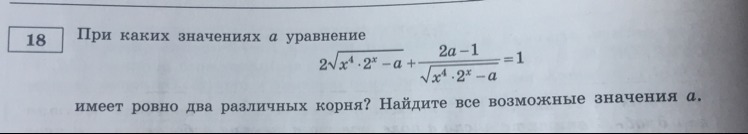
Ответы
Автор ответа:
2
y1,2=¼±✓((1/16)+(1-2a)/2=¼±¼✓9-2a
y≥0 => y==¼+✓¼✓(9-2a)
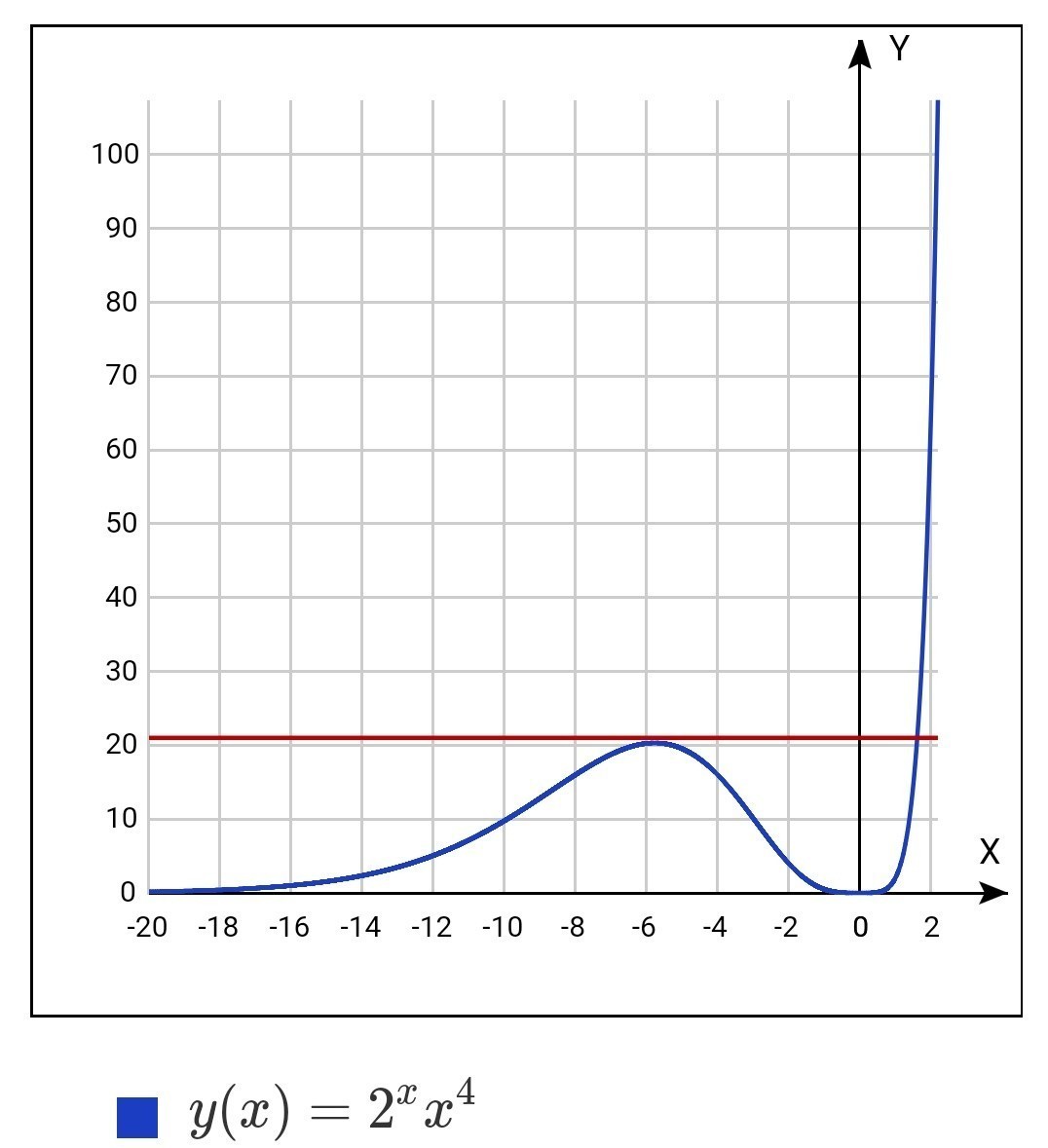
построим
(см рис)
два различных корня уравнение имеет
при
где x(max)- точка максимума y(x)
остаётся найти у'(х)
решить уравнение у'(х)=0
и найти x( max)
((2^x)*x⁴)' = (2^x)'*x⁴+(2^x)*(x⁴)' =
=(2^x)*ln(2)*x⁴+(2^x)*4x³=
=x³(2^x)ln2(x+4/ln2)=0
х(max)= -4/ln2
и решить уравнение (1) для нахождения а
-4/ln2=⅛ (5 + 7a + ✓(9 - 2a))
отсюда находят а
=✓(9 - 2a)
-7a-(5+(32/ln2))=✓(9 - 2a)
возводим в квадрат:
49a²+
+14*(5+(32/ln2))а+(5+(32/ln2))²=9-2a
49а²+(72+(32/ln2))а+
+(5+(32/ln2))²-9=0
а²+((72+(32/ln2))/49)а+
+(5+(32/ln2))²-9=0
a1,2=-((72+(32/ln2))/49)±
±✓[(((72+(32/ln2))/49)²+9-
-(5+(32/ln2))²]
а допустимые значения а
находят из условия 9-2а≥0 или а≤4,5
Приложения:
ksyushakot1999:
извените, а вы можете подсказать как я могу удалить мой не честный ответ?
И потом решить
Похожие вопросы
Предмет: Музыка,
автор: gulsarasaudabaeva33
Предмет: Литература,
автор: maximggfjs
Предмет: Математика,
автор: niyazovamalikusha
Предмет: Информатика,
автор: ilyinavlada