Предмет: Математика, автор: sdgfdhtrhrveter

(34 балла)Задание легкое должно быть)()(())()()()()()()((). В равнобедренном треугольнике, высота, проведенная к боковой стороне делит ее на отрезки 8 и 6 см, считая от вершины. Найдите площадь треугольника.

Ответы

Автор ответа: IrkaShevko

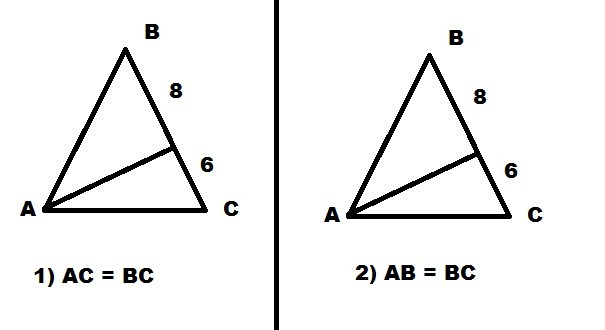
по условию не очень понятно, поэтому рассмотрим два случая (на рисунке)

1) АС = 8 + 6 = 14 (см)

по т. Пифагора высота = √(196 - 36) = √160 = 4√10 (см)

S = 0,5 * 4√10 * 14 = 28√10 (см²)

Ответ: 28√10 см²

2) AB = 8 + 6 = 14 (см)

по т. Пифагора высота = √(196 - 64) = √132 = 2√33 (см)

S = 0,5 * 2√33 * 14 = 14√33 (см²)

Ответ: 14√33 см²

Приложения:

sdgfdhtrhrveter: А в чём ошибка в условии

IrkaShevko: там не ошибка, а просто непонятно от какой вершины

Пеппер: Высота к боковой стороне АВ или ВС может быть проведена или из вершины А, или из вершины С, это не имеет значения для результата. И решение здесь может быть только одно.

IrkaShevko: если внимательно посмотрите на мое решение, то поймете, что я имею в виду не высоту из какой вершины проводить

IrkaShevko: да и очевидно, если бы я разбила на случаи, о которых вы говорите, то ответ бы совпал, а в этих двух разные

Автор ответа: Пеппер

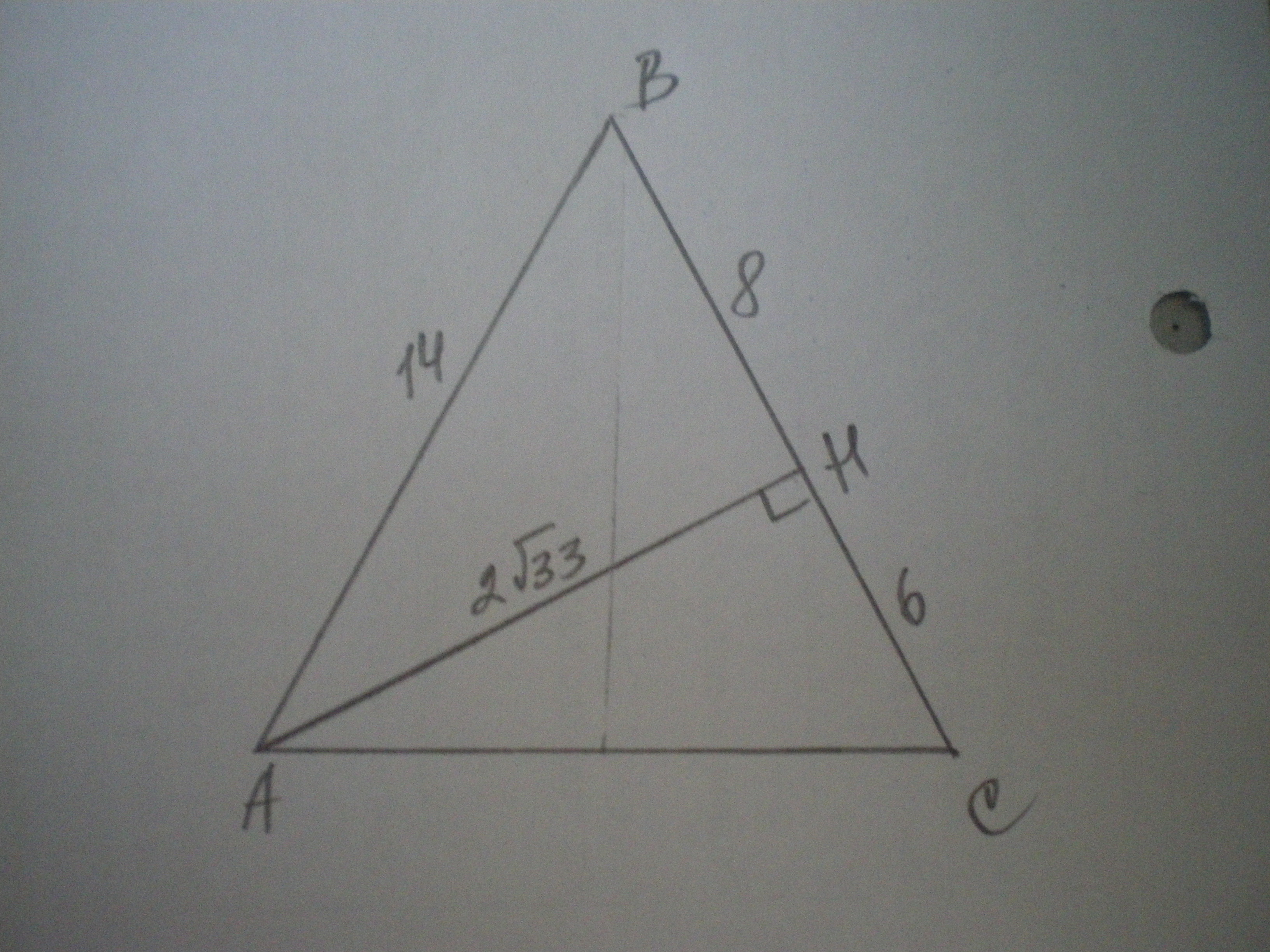
Дано: ΔАВС - равнобедренный, АВ=ВС=14 см, АН - высота, ВН=8 см, СН=6 см. Найти S (АВС).

S= 1\2 * BC * AH

Найдем АН из ΔАВН - прямоугольного;

АН=√(АВ²-ВН²)=√(196-64)=√132=2√33 см

S = 1\2 * 14 * 2√33 = 14√33 см²

Приложения: