Question

Решить уравнение |(x-1)(x-6)|*(|x+2|+|x-8|+|x-3|)=11(x-1)(6-x)
Желательно с пояснением.

Answer 1

$|(x-1)(x-6)|\cdot(|x+2|+|x-8|+|x-3|)=11(x-1)(6-x)$

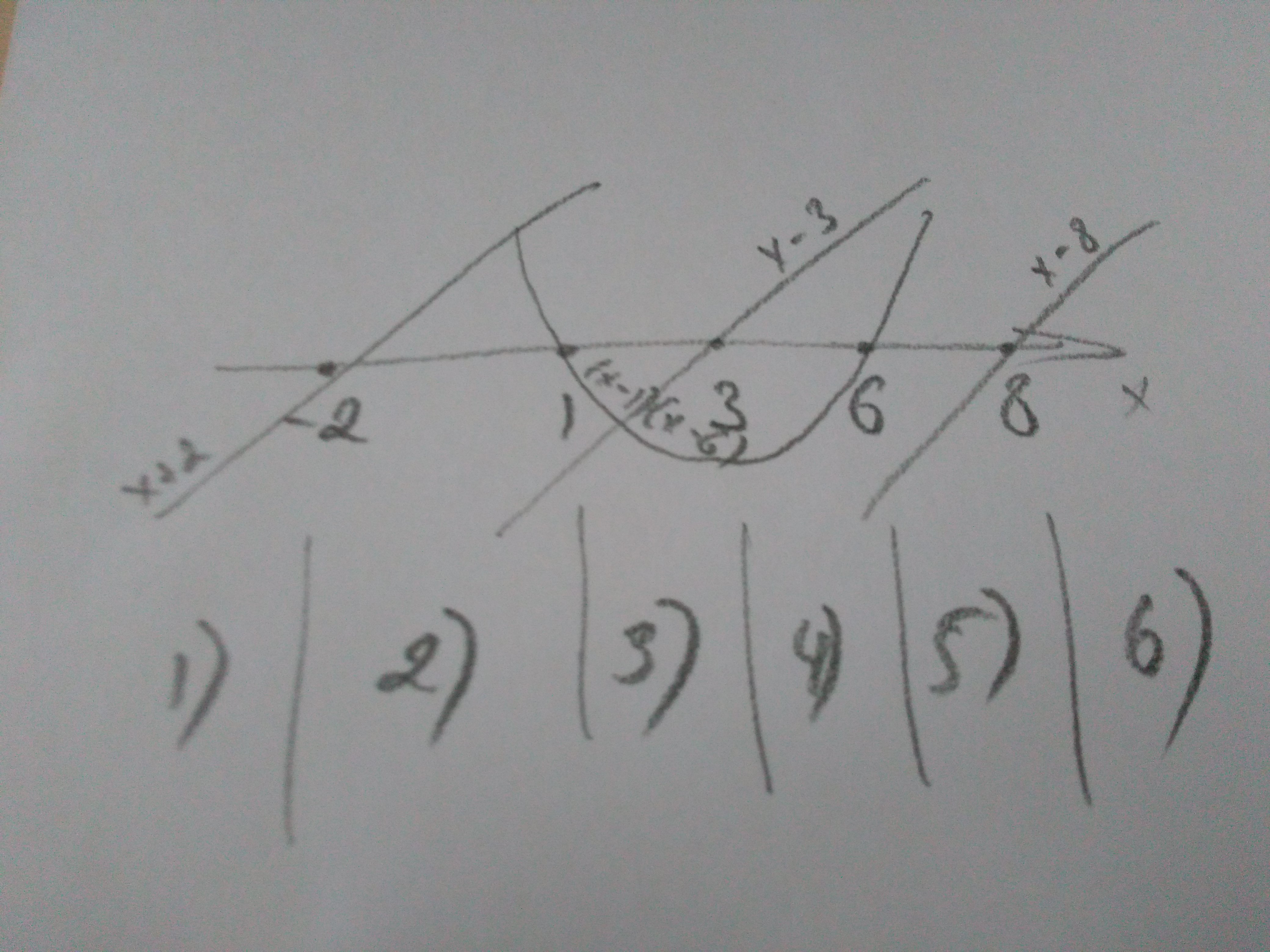
Из-за обилия модулей уравнение придется решать на интервалах. Сразу отметим, что x=1 и x=6 являются решением уравнения, так как обнуляют обе его части. Для удобства для каждого интервала будем делить все уравнение на (x-1)(x-6).

Найдем нули подмодульных выражений

(x-1)(x-6)=0 ⇒ x=1, x=6

x+2=0 ⇒ x=-2

x-8=0 ⇒ x=8

x-3=0 ⇒ x=3

Чтобы не запутаться, используем числовую прямую (в прикрепе)

$1) \ x \in ( - \infty; \ -2)\\ -x-2-x+8-x+3=-11\\ -3x=-20\\ x=\dfrac{20}{3} \notin (- \infty ; \ -2) \\ \\ 2) \ x \in [-2; \ 1]\\ x+2-x+3-x+8=-11\\ -x=-24\\ x=24 \notin [-2; \ 1]\\ \\ 3) \ x \in (1; \ 3)\\ x+2-x+3-x+8=11\\ -x=-2\\ x=2\\ \\ 4) \ x \in [3; \ 6]\\ x+2+x-3-x+8=11\\ x=4\\ \\ 5) \ x \in (6; \ 8)\\ x+2+x-3-x+8=-11\\ x=-18 \notin (6; \ 8)\\ \\ 6) x \in [8; \ + \infty)\\ x+2+x-3+x-8=-11\\ 3x=-2\\ x=-\dfrac{2}{3} \notin [8; \ + \infty)$

Ответ: 1; 2; 4; 6