Question

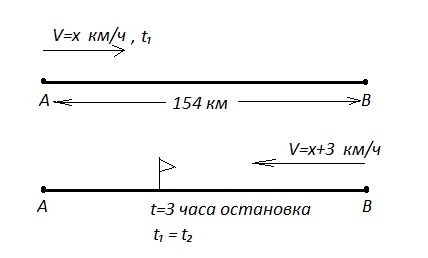
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 154 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 ч. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
(решать не нужно, сделайте пожалуйста рисунок задачи)

Answer 1

х км/ч - скорость велосипедиста из пункта А в пункт В.

(х+3) км/ч - скорость велосипедиста из В в А.

Время из А в В = $t_1=\frac{154}{x}$ часов.

Время изВ в А = $t_2=\frac{154}{x+3}+3$ часов.

$\frac{154}{x}=\frac{154}{x+3}+3\; \; \Rightarrow \; \; \frac{154}{x}=\frac{163+3x}{x+3}\; \; \Rightarrow \; \; 1544(x+3)=x(163+3x)\\\\3x^2+9x-462=0\\\\x_1=-14<0\; ,\; \; x_2=11\\\\x_2+3=11+3=14$

Оевет: 14 км/ч.