Предмет: Алгебра,
автор: adespina2004
Выполните разложение многочленов :
(n-3m)(3m+n)
(2a-3b)(3b+2a)
(8c+9d)(9d-8c)
Разложите на множители :
9m^2-16n^2
64p^2-81q^3
9-b^2c^2
4a^2b^2-1
Ответы
Автор ответа:
0
Автор ответа:
2
--------------------------------------
Вот.
--------------------------------------
Вот.
--------------------------------------
Приложения:
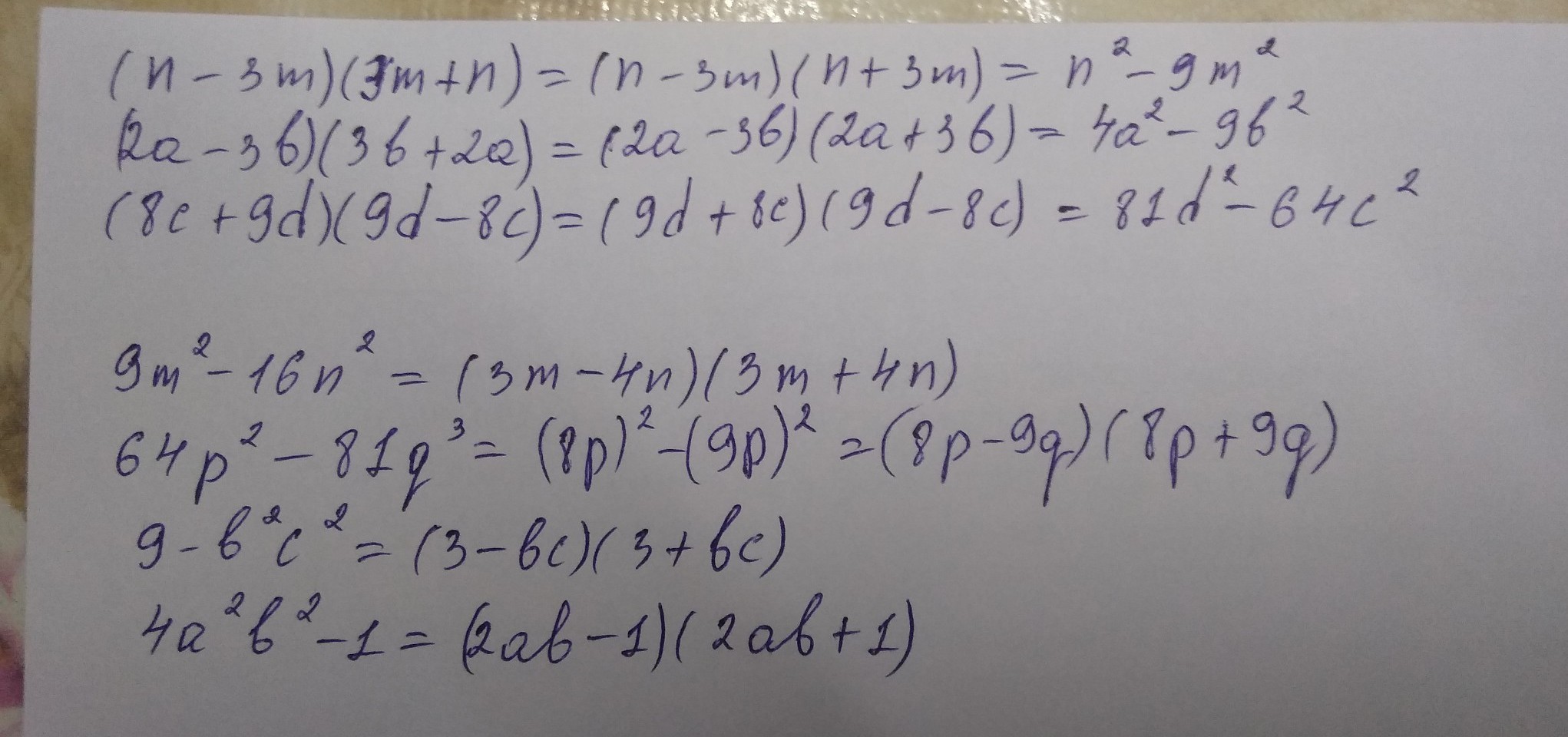
Похожие вопросы
Предмет: Физика,
автор: Lorijyk07
Предмет: Математика,
автор: amirzhanakbarov1
Предмет: Алгебра,
автор: ododkd
Предмет: История,
автор: rogrog