Предмет: Математика,
автор: kryakvalos
помогите,пожалуйста!!!!!!!!!!!!!!!!!
Приложения:
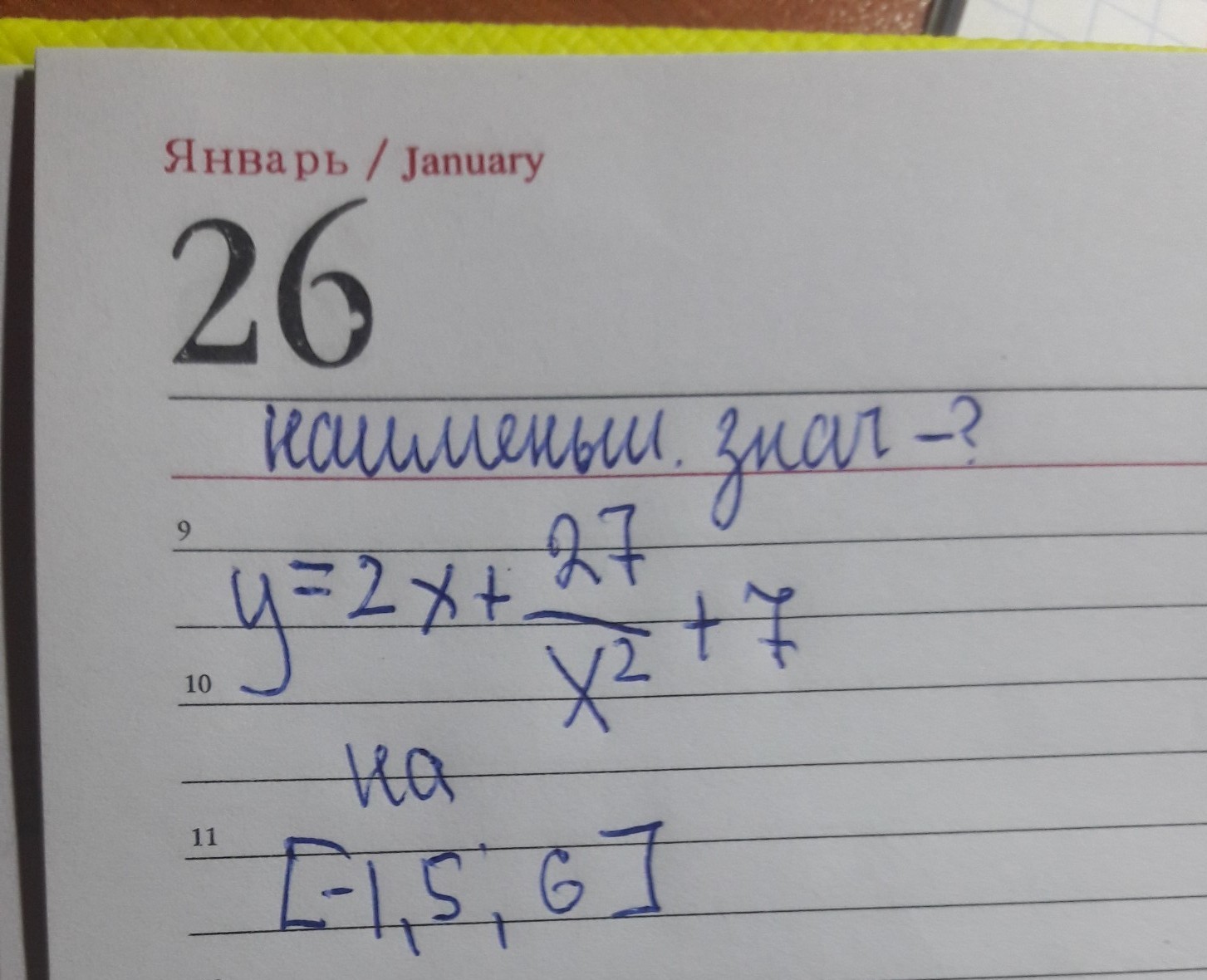
Ответы
Автор ответа:
2
Найдем производную функции
y'=2+27*(-2x/x⁴)=2-54/x³=(2x³-54)/x³
(2x³-54)/x³=0
2x³=54
x=3
Помимо этого, производная функции не определена в точке x=0, которая является точкой разрыва.
Следовательно, критические точки: x=0, x=3.
Определим знаки производной функции
(+)__0___(-)__3__(+)
Следовательно, точка минимума равна 3
y(3)=2*3+27/9+7=16
y(-1,5)=2*(-3/2)+27/(9/4)+7=-3+12+7=16
y(6)=2*6+27/36+7=19¾
Наименьшее значение на отрезке [-1,5; 6] равно 16
y'=2+27*(-2x/x⁴)=2-54/x³=(2x³-54)/x³
(2x³-54)/x³=0
2x³=54
x=3
Помимо этого, производная функции не определена в точке x=0, которая является точкой разрыва.
Следовательно, критические точки: x=0, x=3.
Определим знаки производной функции
(+)__0___(-)__3__(+)
Следовательно, точка минимума равна 3
y(3)=2*3+27/9+7=16
y(-1,5)=2*(-3/2)+27/(9/4)+7=-3+12+7=16
y(6)=2*6+27/36+7=19¾
Наименьшее значение на отрезке [-1,5; 6] равно 16
Похожие вопросы
Предмет: Математика,
автор: aduba485
Предмет: Қазақ тiлi,
автор: b76
Предмет: Другие предметы,
автор: ivankovaanel
Предмет: Математика,
автор: срочно1950
Предмет: Геометрия,
автор: machapoga1502