Предмет: Математика,
автор: 231asd31
система система система
Приложения:
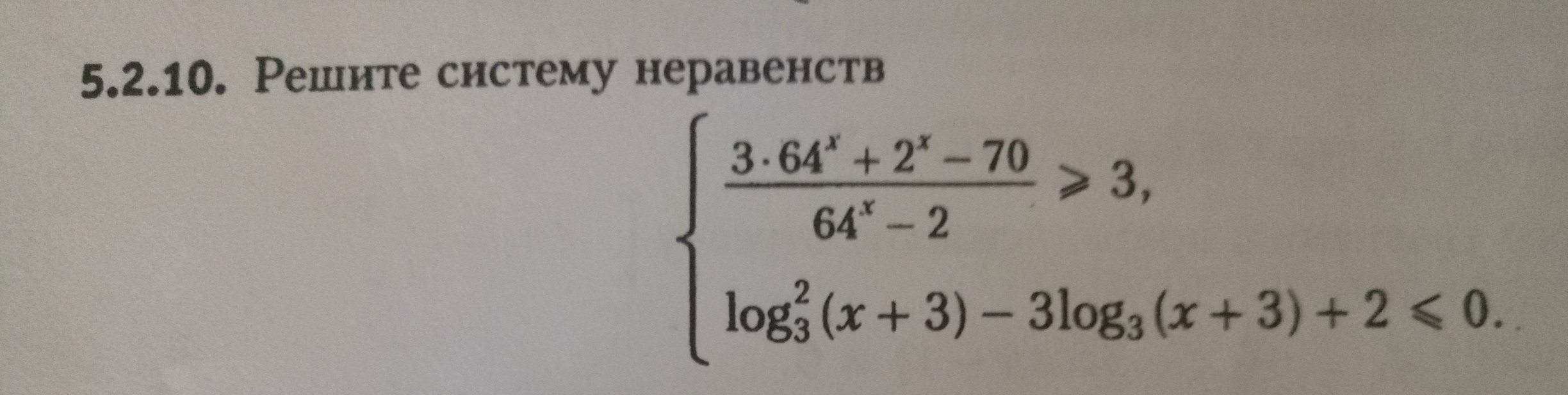
Ответы
Автор ответа:
0
(1) 

__(+)__\(1/6)__(-)__6/__(+)__

(2) ОДЗ: x>-3

__(+)__\0__(-)__6/__(+)__
![x \in [0;6] x \in [0;6]](https://tex.z-dn.net/?f=x+%5Cin+%5B0%3B6%5D)
Найдем пересечение множеств решений неравенств (1) и (2).

__(+)__\(1/6)__(-)__6/__(+)__
(2) ОДЗ: x>-3
__(+)__\0__(-)__6/__(+)__
Найдем пересечение множеств решений неравенств (1) и (2).
Похожие вопросы
Предмет: Математика,
автор: bolatayzere2610
Предмет: Математика,
автор: tupojmatvej024
Предмет: Математика,
автор: viccifrolova22
Предмет: Математика,
автор: парлян