Question

Тело, брошенное под углом к горизонту, достигло максимальной высоты 5 м, а в горизонтальном направлении пролетело 40 м к моменту падения. Под каким углом и с какой скоростью бросили тело? Считайте, что g=10 м/с^2

Answer 1

Дано:

$h = 5$ м

$l = 40$ м

$g = 10$ м/с²

===================

Найти: $\alpha - ?$ $v_{0} - ?$

===================

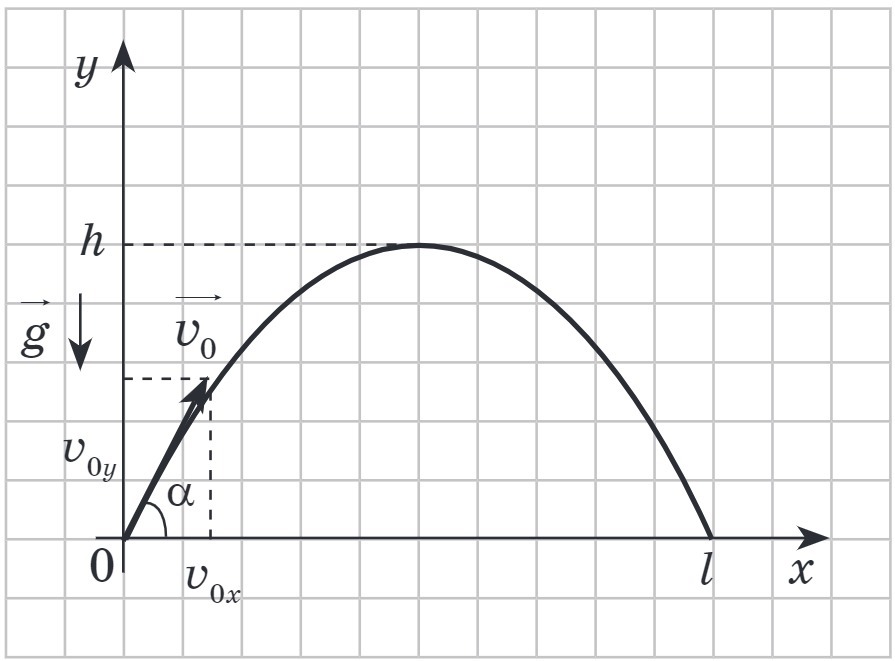
Решение. Движение тела, брошенного под углом к горизонту, является сложным: равномерным по ОХ и свободным падением по OY (см. рисунок).

Максимальную высоту при этом можно определить по формуле (1):

$h = \frac{v_{0}^{2}sin^{2}\alpha}{2g}$ ,

а дальность полёта - по формуле (2):

$l = \frac{2v_{0}sin\alphacos\alpha}{g}$

Разделим уравнение (1) на уравнение (2), получим:

$\frac{h}{l} = \frac{v_{0}^{2}sin^{2}\alpha \cdotp g}{4v_{0}^{2}sin\alpha cos\alpha \cdotp g} \Rightarrow \frac{h}{l} = \frac{tg\alpha}{4}$ , откуда $\boxed{tg\alpha = \frac{4h}{l}}$ .

Выполним расчёты: $tg\alpha = \frac{4\cdotp 5}{20} = \frac{1}{2}$ , тогда $\alpha = arctg\frac{1}{2} \approx 27^{\circ}$.

Из уравнения (1) найдём: $\boxed{v_{0} = \frac{\sqrt{2gh}}{sin\alpha}}$ .

Проверим единицы и определим числовое значение бросания тела:

$[v_{0}] = \sqrt{\frac{_{M} \cdotp _{M}}{c^{2}}} = \sqrt{\frac{_{M^{2}}}{c^{2}}} = \frac{_{M}}{c}$ ;

$v_{0} = \frac{\sqrt{2\cdotp 10 \cdotp 5}}{sin 27^{\circ}} \approx \frac{\sqrt{100}}{0,45} \approx 22,2 \frac{_{M}}{c}$

Ответ: тело бросили с начальной скоростью υ₀ ≈ 22,2 м/с под углом α = 27° к горизонту.