Предмет: Алгебра,
автор: asdasd127
Здравствуйте, объясните, пожалуйста, как решаются подобные уравнения?
Приложения:
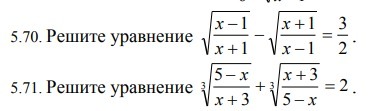
NNNLLL54:
Jдин из корней обозначь новой переменной t, второй корень будет тогда 1/t.
а дальше что? я пробовал так решить, но не получилось ничего
Можете решить, если не сложно, пожалуйста, буду очень благодарен
Ответы
Автор ответа:
1
во 2 примере должно 1 получиться, судя по ответам... Или в ответах опечатка
Да, получится 1, у меня была описка.
Спасибо за поправку
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: alexander01908
Предмет: Математика,
автор: dasha6488
Предмет: Информатика,
автор: Эваааа
Предмет: Геометрия,
автор: smirnovar2016