Предмет: Математика,
автор: Mariaglu2
розвязати рівняння чере 2^x=t
Приложения:
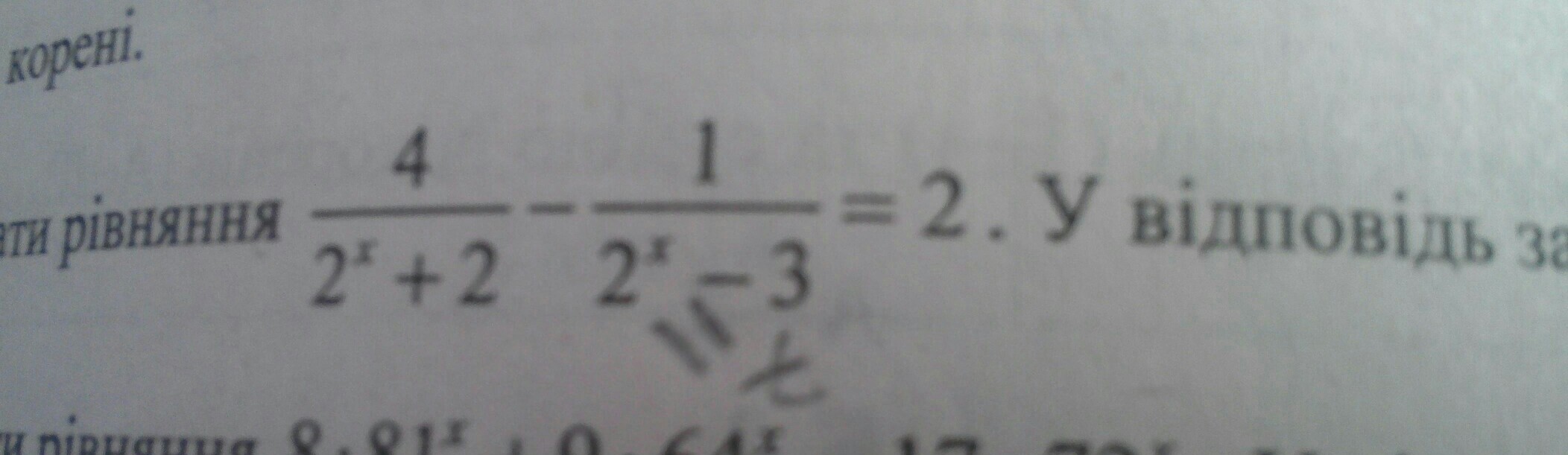
Ответы
Автор ответа:
1
ОДЗ: t + 2 ≠ 0, t ≠ -2
t - 3 ≠ 0, t ≠ 3
Ответ: -1; 1.
Похожие вопросы
Предмет: Русский язык,
автор: levelup638
Предмет: История,
автор: bigaevaalina607
Предмет: Английский язык,
автор: kausararshynkyzy
Предмет: Литература,
автор: nmilkanisn2ay