Question

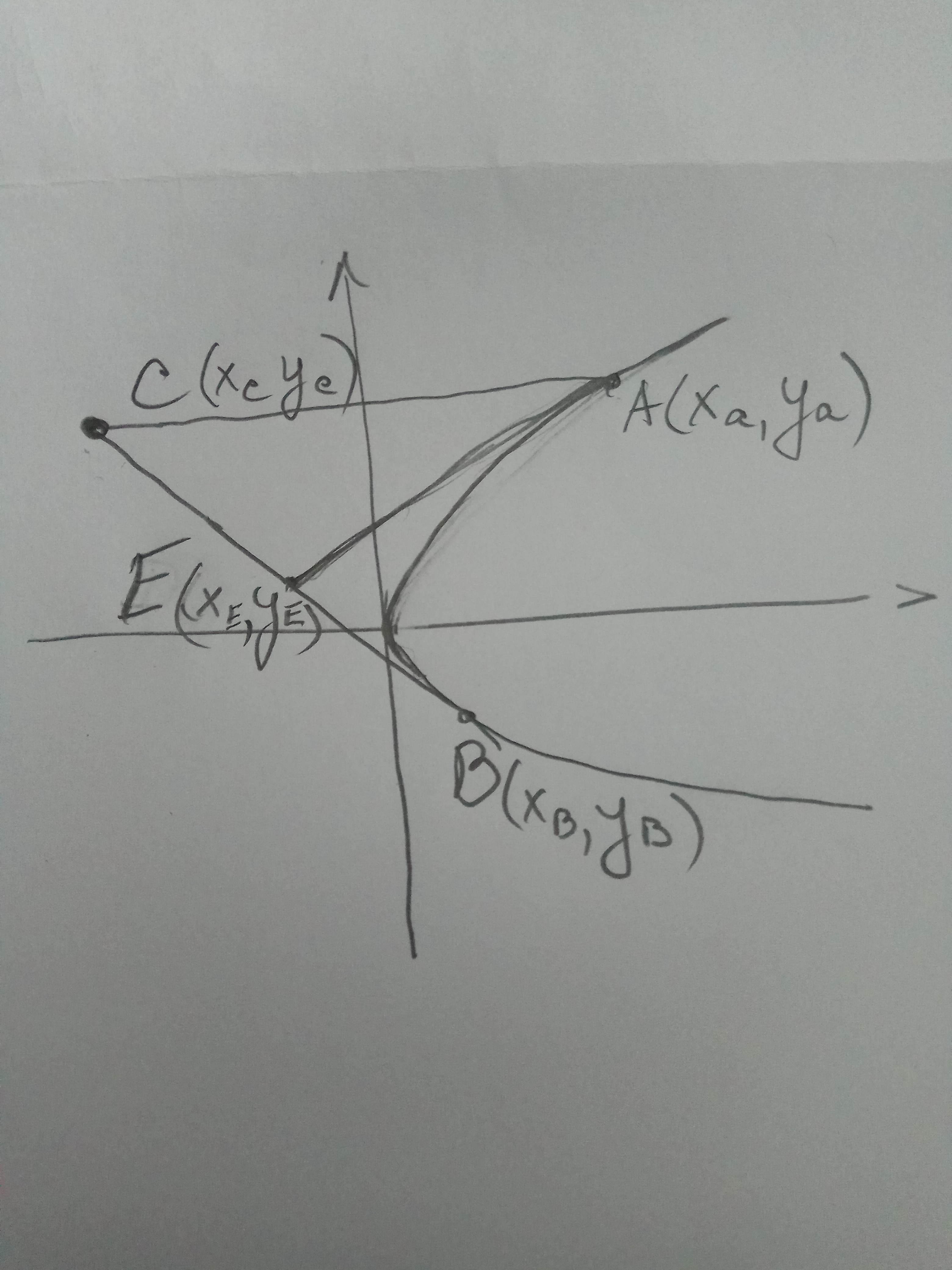
Дано уравнение параболы У² =2Х.Прямая ,касательная к параболе в точке А пересекается в точке Е(Хе,Уе) с прямой, касательной к параболе в точке В. А  - в первой,а В(Хв,Ув)-  в 4 четверти.Через точку А(Ха,Уа) провели прямую,которая пересекает прямую ВЕ в точке С(Хс,Ус) так,что СЕ=ЕВ. 1) покажи,что Уе(Уа-Ув)=Ха-Хв 2) покажи,что СА параллельна оси Х.

Answer 1

1)

Воспользуемся свойствам параболы, а именно если M(x0,y0) точка на параболе, то касательная к ней уравнение имеет вид y*y0=p(x+x0)

Так как y^2=2px=2x (каноническое уравняете параболы) откуда p=1

Пусть координаты

A(x(a), y(a)) =A(x(a), sqrt(2xa)) (после подстановки в y^2=2x)

Так как B находится в четвёртой четверти то

B(x(b), y(b)) = B(x(b), -sqrt(2x(b))

Тогда касательная к точке A и B в общем в виде

{y*ya=x+x(a)

{y*y(b)=x+x(b)

Точка их пересечения (решения) есть точка E(x(e),y(e)

Откуда y*y(a)-x(a) = y*y(b)-x(b)

y(E)=(x(a)-x(b))/(y(a)-y(b))

2) для того чтобы доказать что CA || OX надо доказать что координата точки C по оси OY равна координате точки A по оси OY или y(a)

Так как E середина, то

y(c)+y(b)=2y(e)

y(c)=2y(e)-y(b) = 2*(x(a)-x(b))/(y(a)-y(b)) - y(b)

Подсталвяя y(a)=sqrt(2x(a)) и y(b)=-sqrt(2x(b))

Откуда y(c) = sqrt(2x(a)) = y(a)

Значит AC || OX