Question

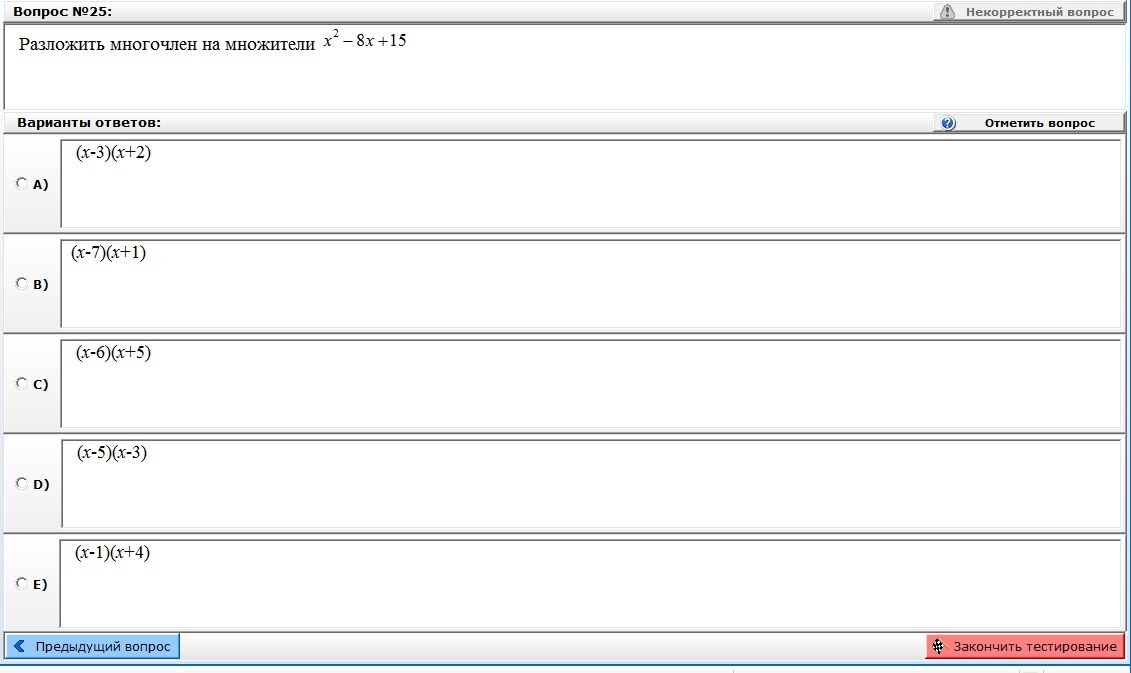
Разложить многочлен на множители
Прошу, можно пожалуйста с объяснением буду благодарен

Answer 1

х²-8х+15=х²-8х+16-1=(х-4)²-1=(х-4+1)(х-4-1)=(х-3)(х-5)

в исходном выражении сначала выделили полный квадрат

Answer 2

а я очень люблю теорему Виета... (не будем удлинять название словом "обратная"))

квадратный трехчлен можно разложить на множители через корни x₁ и x₂:

a*x² + bx + c = a*( x - x₁ )*( x - x₂ )

произведение корней = +15

сумма корней = +8 (подбираем числа устно --это 5 и 3)

x² - 8x + 15 = ( x - 3 )*( x - 5 )

и всегда делаем проверку--устно раскрываем скобки...