Предмет: Математика,
автор: purpurmeow
Решите пару предельчиков, пожалуйста:)
Приложения:
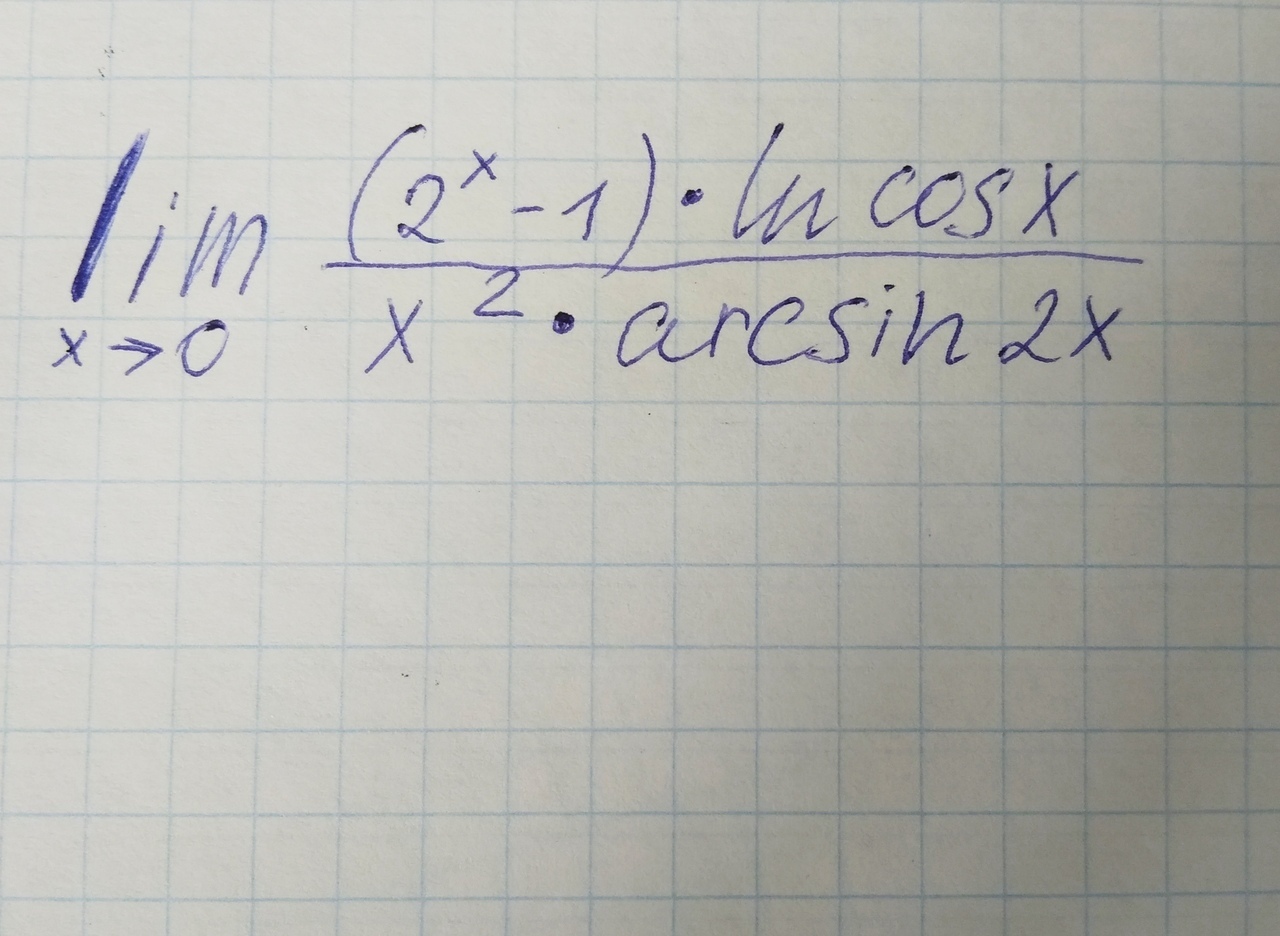
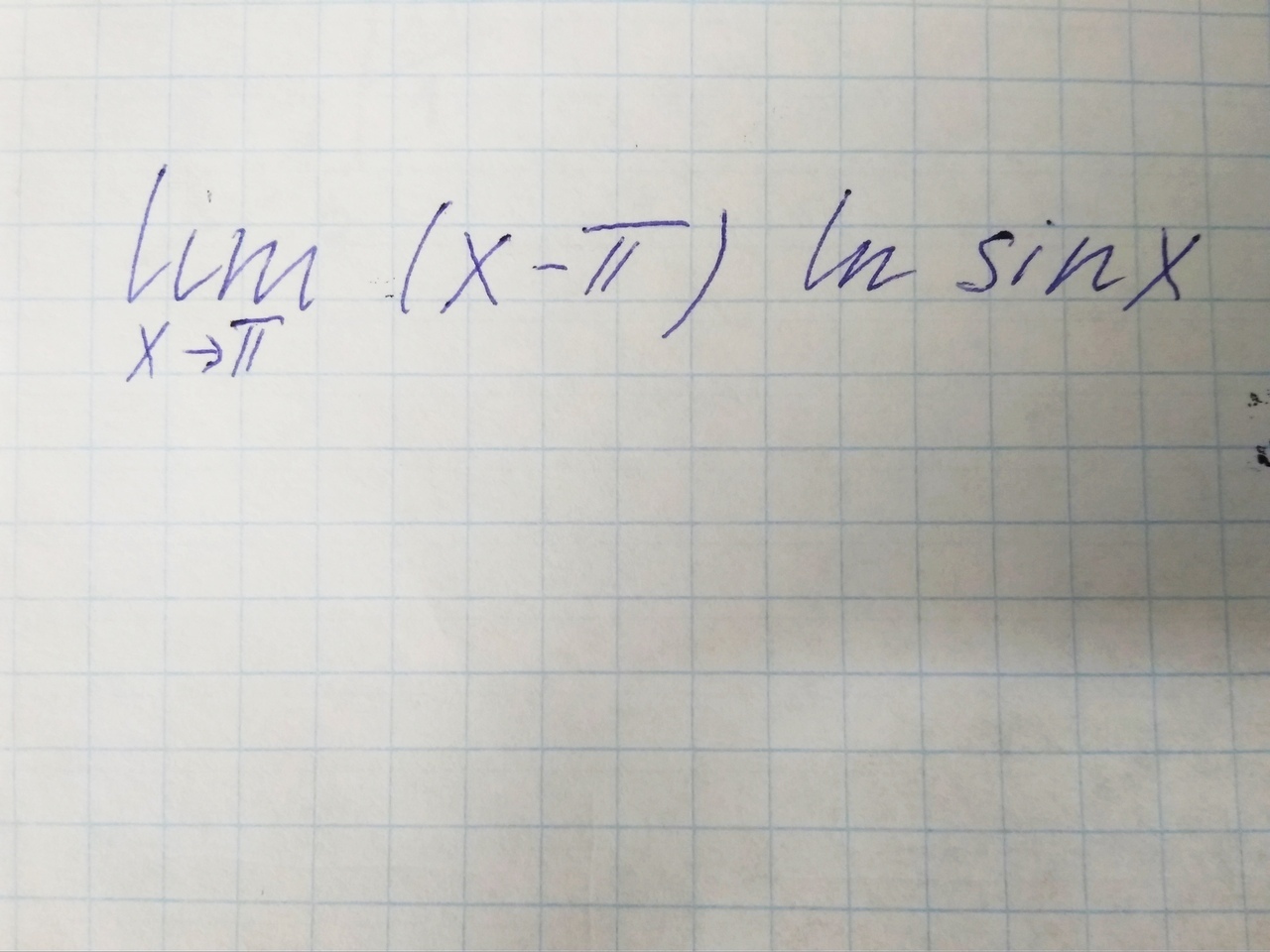
Ответы
Автор ответа:
1
1)

1.

2.


Ответ: - ln(2)/4.
2)

Ответ: 0
1.
2.
Ответ: - ln(2)/4.
2)
Ответ: 0
Похожие вопросы
Предмет: Математика,
автор: vorobevasofa414
Предмет: Геометрия,
автор: anastasiaslabko37
Предмет: Математика,
автор: alizhanaslanpro2010
Предмет: Химия,
автор: igorku2010
Предмет: Алгебра,
автор: Lebed01