Предмет: Алгебра,
автор: Djasurxon
если х<-2, то упростите данное выражение!, помогите пожалуйста
Приложения:
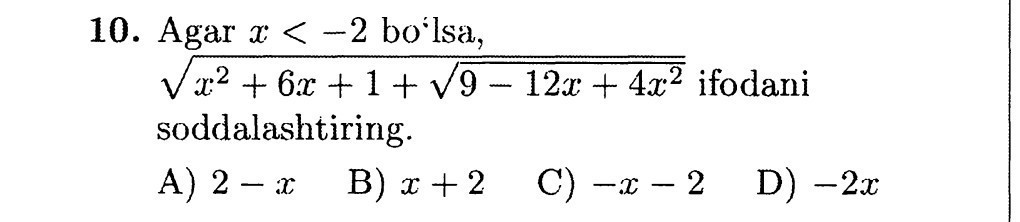
ivanspraguepaar7t:
4x^2-12x+9= (2x-3)^2. Корень из квадрата => модуль. Раскрываем его для x<-2 и упрощаем главный корень.
да я пробовал, но главный корень не упрощается
Модуль раскрывается отрицательно => под главным корнем будем иметь x^2+4x+4= (x+2)^2
аа спс огромное)
Полученный модуль |x+2|, дающий -x-2 при x<-2
Удачи вам!
спасибо и вам
Ответы
Автор ответа:
2
Но по условию х < - 2 , значит , 3 - 2х > 0
ОТВЕТ: С
Похожие вопросы
Предмет: Геометрия,
автор: gorobcovvd
Предмет: Русский язык,
автор: amiraorynbasarova59
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Литература,
автор: pomka27
Предмет: Математика,
автор: sz122271214