Предмет: Математика,
автор: Аноним
1 / cos²x = 2tg²x
....
Ответы
Автор ответа:
3
решение на фото внизу
Приложения:
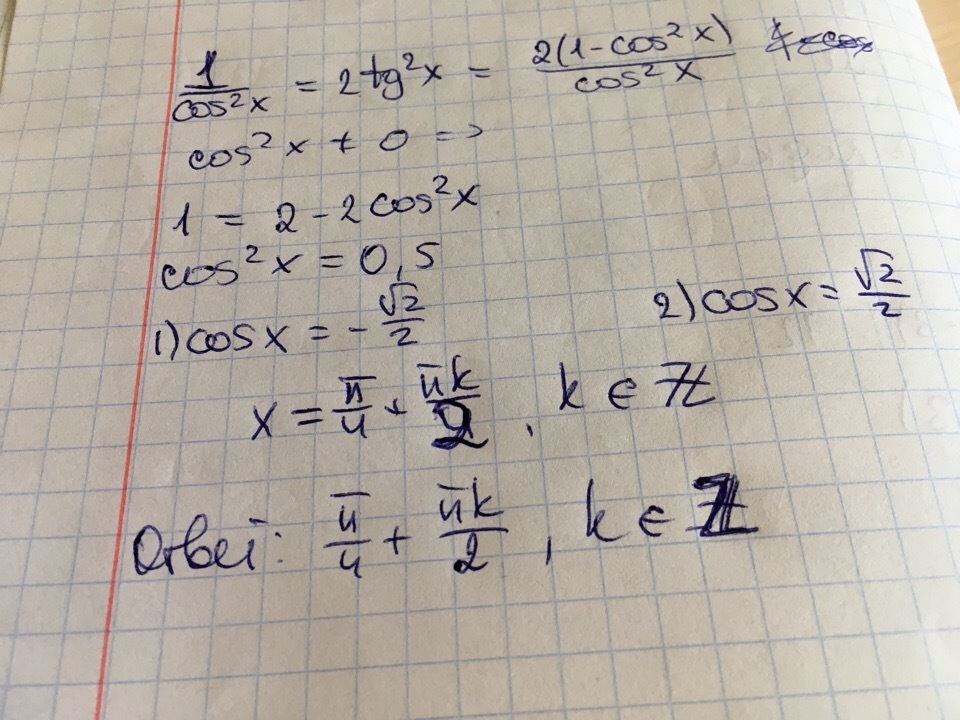
Автор ответа:
17
Зная, что , имеем
Аноним:
А обратную махинацию нельзя сделать? т.е. 1 / cos²x представить как 1+tg²x и искать корни для тангенса?
Можно)
Так из-за этого ответ не сходится(
x=+- п/2 + пn
ой, п/4
1+tg^2x=2tg^2x
tg^2x=1
tgx=±1
tgx=±pi/4+pi*n
tg^2x=1
tgx=±1
tgx=±pi/4+pi*n
Но ответ является верным
Для каждого способа решений есть другой ответ и причем правильный)
Подставьте п/4 и получите 2=2
Ясно, спасибо большое)
Похожие вопросы
Предмет: Литература,
автор: burick789
Предмет: Информатика,
автор: porosaryona
Предмет: Биология,
автор: meowwUwU
Предмет: Алгебра,
автор: Соня1455
Предмет: Математика,
автор: vika522